Если фирма получила кредит в размере 2000 сроком на 2 года под 10 годовых
Обновлено: 22.04.2024
Употребление термина «процент» в России начинается с XVIII в. Это понятие впервые ввёл Пётр I. Однако считается, что подобные вычисления начали применяться ещё в Смутное время — как результат первой в мировой истории привязки чеканных монет 1 к 100, когда рубль сначала состоял из 10 гривенников, а позже из 100 копеек.
Долгое время под процентами понимались исключительно прибыль или убыток на каждые 100 рублей. Проценты применялись только в торговых и денежных сделках. Затем область их применения расширилась.
Например, можно услышать фразы «в выборах приняли участие 60% избирателей», «успеваемость в классе 95%», «банк начисляет 12% годовых», «молоко содержит 1,5% жира», «материал состоит из 100% хлопка», «скидка составляет 5%», «на карту начисляется кэшбэк 3,5%» и так далее.
Современная жизнь делает задачи на проценты актуальными. Вопросы инфляции, девальвации, повышения цен, снижения покупательной способности касаются каждого человека. Школьники — будущие участники финансового рынка, налогоплательщики, вкладчики, заёмщики, поэтому уже на начальных ступенях образовательной системы необходимо вводить финансовое обучение.
Вполне закономерно, что каждый из нас хочет получать дополнительный доход. Банковские вклады (депозиты) — простой способ не только сохранить, но и приумножить свои сбережения. У всех банков разные процентные ставки, которые зависят от условий хранения денег: валюты, сроков, суммы размещения, возможности снятия и пополнения счёта, капитализации процентов.
Давайте разберёмся с понятием «процентная ставка по вкладу» и видами процентов.
Процентная ставка — это процент, который клиент получает за размещение средств на вкладе на определённый срок. Обычно подразумевается годовая процентная ставка. Если срок вклада больше или меньше года, для расчёта дохода необходимо привести ставку к реальному сроку вклада.
Однако выгода банковского вклада оценивается не только по процентной ставке. Большое влияние на доходность оказывает способ начисления процентов. В финансовой сфере существует понятие простого и сложного процента.
Простые проценты начисляются по следующей формуле:
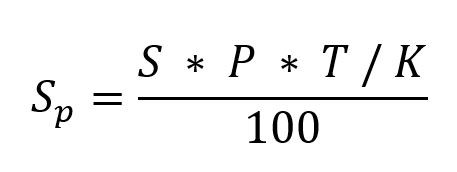
Sp — выплаченные проценты;
S — первоначальная сумма вложений;
P — годовая ставка;
T — количество дней вклада;
K — количество дней в году — 365 или 366.
Пример 1. Вкладчик размещает 1 января 2021 г. (не високосный год) вклад в размере 350 000 руб. под 4,7% годовых сроком на 9 месяцев (273 дня).
Процентный доход по данному вкладу составит:
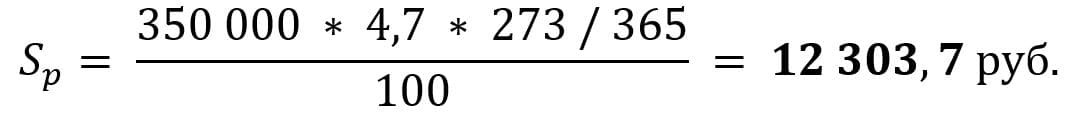
Капитализированный (причисленный) процент — процент, начисляемый на сумму вклада и сумму ранее начисленных по вкладу процентов с учётом срока вклада с определённой договором банковского вклада периодичностью.
Чаще всего банки предлагают программы с ежемесячной капитализацией, при которой процентный доход рассчитывается по формуле:
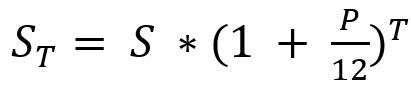
ST — итоговый доход, то есть размер вклада на конец срока, включая сумму открытия и начисленный процент;
S — начальный депозит;
P — годовая ставка, разделённая на 100 (выраженная десятичной дробью);
T — срок договора в месяцах.
Рассчитаем итоговую сумму с теми же исходными данными:
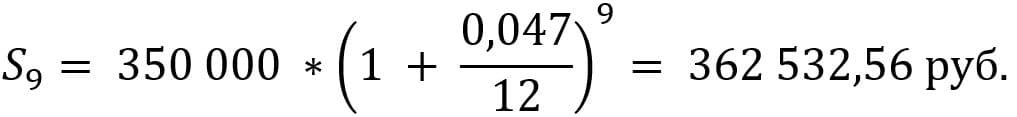
Процентный доход составит: 362 532,56 – 350 000 = 12 532,56 руб.
При начислении вознаграждения каждый квартал, а не раз в месяц, воспользуемся формулой:
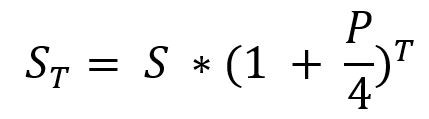
где Т — количество кварталов в сроке, остальные обозначения прежние.
Рассчитаем тот же вклад на конец срока.
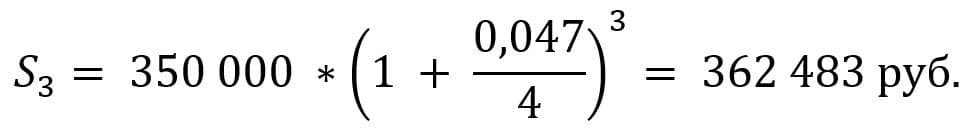
Доход в виде процентов в данном случае составит 12 483 руб.
В этом примере выгоднее оказался депозит со сложной процентной ставкой при условии ежемесячной капитализации.
Пример 2. Иван Иванович (И.И.) за внедрение рационализаторского предложения получил премию в размере 200 000 руб. Увидел по телевизору рекламу банка Х о супервыгодных условиях вклада под 6% годовых с условием размещения депозита на три года.
Рассчитаем доход И.И. от данного предложения при условии простых процентов.
Ежегодный доход составит: 200 000 * 6 / 100 = 12 000 руб.
Доход за три года: 36 000 руб.
К концу третьего года на счёте И.И.: 200 000 + 36 000 = 236 000 руб.
Таким образом, для расчёта суммы вклада через n лет под P% можно воспользоваться формулой:
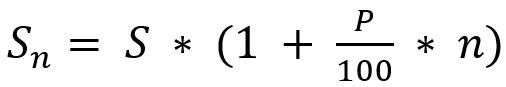
Выполним расчёт дохода И.И. при условии использования сложных процентов с капитализацией в конце года.
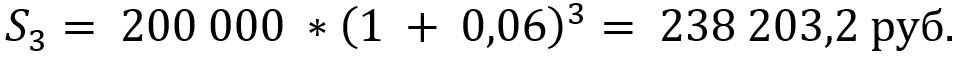
Доход на конец срока в данном случае составит 38 203,2 руб.
Интересно увидеть доход с ежемесячной капитализацией, вот расчёт:
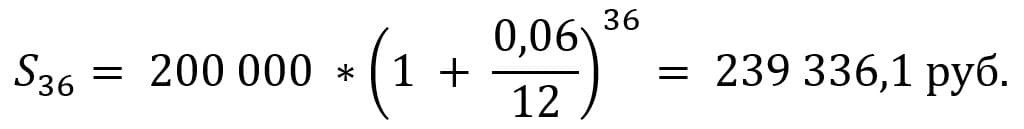
Доход за три года составит 39 336,1 руб.
На что обратить внимание
Мы на примерах показали различие между простой и сложной процентными ставками. Представленные расчёты убеждают в эффективности сложной процентной ставки.
Следует учесть: чем дольше срок размещения депозита, тем выше ставка. Поэтому необходимо сравнивать условия с фактической ставкой, применяемой по выбранным условиям в выбранном банке, и анализировать предложения по вкладам, обращая внимание на все условия, касающиеся будущей доходности.
Задача 6.1. Банк согласился учесть вексель на сумму 10 тыс. руб. за 60 дней до срока погашения. Определите сумму вексельного кредита, если ставка дисконта составляет 14% годовых.
Дисконтированную сумму вексельного кредита определяют по формуле
Задача 6.2. Определите сумму средств к погашению кредита в размере 2 тыс. руб., полученного на 30 дней под 16% годовых.
Наращенную сумму долга с учетом процентов за кредит рассчитывают по формуле
Задача 6.3. Определите сумму вклада сегодня, чтобы через два года иметь накопления в размере 10 млн руб. Годовая ставка процента составляет 6%.
Дисконтированную сумму вклада вычисляют по формуле
Задача 6.4. Банк принял к учету вексель в сумме 100 млн руб. за 60 дней до наступления срока погашения. Определите сумму вексельного кредита при годовой ставке дисконта 16%.
Дисконтированную сумму вексельного кредита определяют по формуле
Задача 6.5. Используя формулу простых процентов, определите сумму средств к погашению краткосрочного кредита в размере 100 млн руб. через 30 дней. Годовая ставка процента составляет 16%.
Наращенную сумму долга с учетом процентов за кредит рассчитывают по формуле
Задача 6.6. Используя формулу сложных процентов, определите сумму депозитного вклада в размере 100 млн руб. через два года при ежегодном начислении 6% годовых.
Наращенную сумму депозитного вклада вычисляют по формуле
F = P (1 + i : 100) n ,
Задача 6.7. Используя формулу сложных процентов, найдите сумму депозитного вклада в размере 100 млн руб. через два года при полугодовом начислении процентов. Годовая ставка составляет 6%.
Наращенную сумму депозитного вклада определяют по формуле
Задача 6.8. Используя формулу дисконтирования, определите размер вексельного кредита при учете векселя в сумме 100 млн руб. за 100 дней до наступления срока погашения. Годовая ставка дисконта составляет 6%.
Дисконтированную сумму вексельного кредита рассчитывают по формуле
Задача 6.9. Используя формулу дисконтирования, определите величину приведенного дохода от инвестиций за два года, если в первом году получено 100 млн руб., во втором — 200 млн руб. Годовая ставка дисконта составляет 16%.
Приведенный доход от инвестиций вычисляют по формуле
Задача 6.10. Определите сумму средств к погашению краткосрочного кредита в размере 100 млн руб. через 18 дней при годовой ставке процента 16%.
Наращенную сумму долга с учетом процентов за кредит определяют по формуле
Задача 6.11. Определите сумму депозитного вклада в размере 100 млн руб. через два года при ежегодном начислении 10% годовых.
Наращенную сумму депозитного вклада рассчитывают по формуле
F = P (1 + i : 100) n ,
Задача 6.12. Определите сумму депозитного вклада под 10% годовых в размере 100 млн руб. через два года при полугодовом начислении процентов.
Наращенную сумму депозитного вклада вычисляют по формуле
Задача 6.13. Распределению среди акционеров подлежит 20 млн руб. чистой прибыли предприятия. В обращении находится 1000 обыкновенных акций. Дивиденды, выплаченные по привилегированным акциям, составили 5 млн руб. Определите доход (прибыль) на одну акцию.
Доход на одну акцию определяют как частное от деления всей суммы денежных средств, направляемых на выплату дивидендов по обыкновенным акциям, на число акций, находящихся на руках акционеров:
Задача 6.14. Предприятие выплатило по акциям 100 млн руб. дивидендов. Рыночная стоимость акций составляет 4 млрд руб. Определите текущую доходность (дивидендный доход) акций предприятия (в обращении находится 40 тыс. акций).
Контрольные задачи
Задача 7.1. Определите оптовую цену предприятия Цопт.пр, оптовую цену сбытовых организаций Цопт.сб.орг, государственную розничную цену Цр, если: плановая себестоимость единицы промышленной продукции Спл = 150 тыс. руб.; прибыль, приходящаяся на единицу продукции, Пед = 37,5 тыс. руб.; налог на добавленную стоимость НДС = 25,2 тыс. руб.; текущие издержки и прибыль сбытовых организаций ТЗсб + Псб = 5,6 тыс. руб.; текущие издержки и прибыль торгующих организаций ТЗт + Пт = 11,7 тыс. руб.
Цопт.пр = С + П + НДС.

Задача 7.2. Определите верхний предел цены нового оборудования, если: цена базисной модели Цб = 120 тыс. руб.; производительность базисной модели Qб = 1000 шт./ч; производительность новой модели Qн = 1000 шт./ч; норма амортизации базисной модели На.б = 0,2; норма амортизации новой модели На.н = 0,2; нормативный коэффициент эффективности Ен = 0,25; эксплутационные издержки базисной модели Иб = 40 тыс. руб.; эксплутационные издержки новой модели Ин = 30 тыс. руб.; экономия капитальных вложений К = 10 тыс. руб.
Верхний предел цены нового оборудования, руб.:

Цв = Цб x Qн : Qб (На.б + Ен) : (На.н + Ен) + (Иб - Ин) : (На.н + Ен) ± К.
1. 15 мая открыт сберегательный счет в сумму (400+10n) руб. под процентную ставку 8% годовых, 12 июля на счет было дополнительно внесено 200 руб.; 12 сентября со счета была снята сумма 100 руб., а 18 ноября счет был закрыт. Определить общую сумму, полученную вкладчиков при закрытии счета. Использовать английскую практику начисления процентов. Год – невисокосный.
P = 400+1019 = 590 руб.
Для решения задачи воспользуемся следующей формулой:
Где S – наращенная сумма;
Р – первоначальная сумма;
I – простая процентная ставка;
T – срок начисления процентов в днях;
К – количество дней в году.
15.05 - 135 день в году;
12.07 - 193 день в году;
12.09. – 255 день в году;
18.11 - 322 день в году.
S1 = 590 597,5 руб.
S2 = 597,5+200 808,34 руб.
808,34 – 100 = 708,34 руб.
S3 = 708,34 718,74 руб.
Ответ: при закрытии счета вкладчик получит 718,74 руб.
2. Долговое обязательство в сумме (2000+100n) руб., должно быть погашено через 90 дней с процентами (10 % годовых). Владелец обязательства учел его в банке за 15 дней до наступления срока по учетной ставке 12%. Найти сумму, полученную после учета векселя.
Р1 =2000+10019 = 3900 руб.
Сначала рассчитаем наращенную сумму долгового обязательства, используя следующую формулу:
Где S – наращенная сумма;
Р – первоначальная сумма;
I – простая процентная ставка;
T – срок начисления процентов в днях;
К – количество дней в году.
S = 39003997,5 руб.
Теперь можем рассчитать сумму, полученную после учета векселя, используя следующую формулу:
Где d - простая учетная ставка
P = 3997,53977,51 руб.
Ответ: сумма, полученная после учета векселя, равна 3977,51 руб.
3. Клиент внес в банк (2000+100n) руб. под 9 % годовых. Через два года и 270 дней он изъял вклад. Определить полученную им сумму при использовании банком сложных процентов и смешенного метода.
P=2000+10019 = 3900 руб.
N = 2 года 270 дней
Если использовались сложные проценты, наращенную сумму определим помощью следующей формулы:
Где S – наращенная сумма;
Р – первоначальная сумма;
I – простая процентная ставка;
N – срок начисления процентов.
S = 390039004942,96 руб.
По смешенному методу:
Где a – целое число лет;
B - дробное число лет.
S = 3900 4946,36 руб.
Ответ: полученная клиентом сумма равна при использовании банком сложных процентов – 4942,96 руб., смешанного метода – 4946,36 руб.
4. Определить эффективную ставку сложных процентов, чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки j%, при ежеквартальном начислении процентов (m=4; j = (5+n)%).
J = 5+19 = 24% = 0,24
Эффективная процентная ставка определяется по следующей формуле:
Где j – номинальная ставка;
M – период начисления процентов.
Iэф = 0,2625 или 26,25%
Ответ: эффективная ставка сложных процентов равна 26,25%
6. Кредит в (2000+100n) руб. выдан на два года. Реальная доходность должна составлять 6% годовых (сложные проценты). Расчетный уровень инфляции – 16% в год. Определить ставку процентов при выдаче кредита, а также наращенную сумму.
Р = 2000+10019 = 3900 руб.
Брутто-ставка по сложной процентной ставке определяется по следующей формуле:
Где i – реальная доходность;
- годовой темп инфляции
R = 0,06 + 0,16 + 0,060,16 = 0,2296 или 22,96%
Наращенную сумму определим по формуле:
Где S – наращенная сумма;
Р – первоначальная сумма;
I – простая процентная ставка;
N – срок начисления процентов.
S = 39005896,47 руб.
Ответ: ставка процентов при выдаче кредита равна 22,96%, наращенная сумма – 5896,47 руб.
7. Объединяются три ренты со сроками 7,4,9 лет; члены ренты равны между собой – R = 2000+100n руб.; процентные ставки так же равны - i = 0,08. Член консолидированной ренты установлен в размере 3R руб.; процентная ставка сохраняется. Определить срок новой ренты.
R1 = R2 = R3 = 2000+10019 = 3900 руб.
R0 = 3R = 33900 = 11700 руб.
Срок консолидированной ренты определим по следующей формуле:
Где - современная стоимость k-й заменяемой ренты.
А1 = 390020305 руб.
А2 = 390012917 руб.
А3 = 390024363 руб.
Ак = 20305 + 12917 + 24363 = 57585 руб.
Ответ: срок новой ренты равен 6,25 лет
8. На модернизацию предприятия получен долгосрочный кредит сроком на 10 лет, погашение которого будет производиться на следующих условиях: в первые пять лет платежи в размере (2000+100n) руб. вносятся каждые полгода под 8% годовых. Следующие три года платежи в размере (4000+100n) руб. вносятся также по полугодиям под 10% годовых. Последние два года платежи в размере (6000+100n) руб. вносятся ежеквартально под 10% годовых. В течение всего срока ренты проценты начисляются раз в году. Определить наращенную сумму и величину кредита.
R1 = 2000+10019 = 3900 руб.
R2 = 4000+10019 = 5900 руб.
R3 = 6000+10019 = 7900 руб.
Наращенная сумма ренты определяется по следующей формуле:
Где S – наращенная сумма;
R – размер платежа;
I – процентная ставка;
N – срок кредита;
P – количество платежей в год.
S1 = 3900 46900 руб.
S2 = 5900 39855 руб.
S3 = 7900 69125 руб.
Sобщ = 46900+39855+69125 = 155880 руб.
Величину кредита определим как современную стоимость каждого потока платежа
А1 = 3900 31942 руб.
А2 = 5900 29944 руб.
А3 = 7900 57128 руб.
А = 31942 + 29944 + 57128 = 119014 руб.
Ответ: наращенная сумма равна 155880 руб., величина кредита – 119014 руб.
9. Предоставлен потребительский кредит в размере (1000+100n) руб. на срок шесть месяцев под 12% годовых с ежемесячными погашением. Составить план погашения кредита. Воспользоваться «правилом 78». Сравните с графиком равномерных выплат процентов.
P = 1000+10019 = 2900 руб.
N = 6 месяцев = 0,5 года
Наращенная сумма долга в конце периода составит:
S = 2900(1+0,50,12) = 3074 руб.
Сумма начисленных процентов:
I = 29000,50,12 = 174 руб.
Найдем сумму порядковых номеров месяцев:
Из первого платежа в счет уплаты процентов идет Общей суммы начисленных процентов:
Сумма, идущая на погашение долга:
512 – 50 = 462 руб.
Составим план погашения.
Доля погашаемых процентов
Сумма погашения процентных платежей, руб.
Сумма погашения основного долга, руб.
Остаток основного долга на начало месяца, руб.
График погашения ссуды с погашением основного долга в конце срока и равномерной выплатой процентов (все данные в тыс. руб.)
Сумма погашения процентных платежей, руб.
Сумма погашения основного долга, руб.
Остаток основного долга на начало месяца, руб.
Всего выплаты в банк
10. Получен кредит в сумме 10000n руб. сроком на семь лет. Процентная ставка изменяется по годам в следующем порядке:
Составьте план погашения кредита.
34035,65 - 1900000,06 = 22635,65 руб.
D2 = 190000 – 22635,65 = 167364,35 руб.
34035,65 – 167364,350,06 = 23993,79 руб.
D3 = 167364,35 – 23993,79 = 143370,56 руб.
37820,79 – 143370,560,1 = 23483,73 руб.
D4 = 143370,56 – 23483,73 = 119886,83 руб.
37820,79 – 119886,830,1 = 25832,11руб.
D5 = 119886,83 - 25832,11 = 94054,72 руб.
39159,59 – 94054,720,12 =39159,59-11286,57 = 27873,02 руб.
D6 = 94054,72 - 27873,02 = 66181,7 руб.
39159,59 – 66181,70,12 =39159,59-7941,8 = 31217,79руб.
D7 = 66181,7 – 31217,79 = 34963,91 руб.
39159,59 – 34963,910,12 =39159,59- 4195,67 = 34963,92 руб.
Составим план погашения:
Сумма долга на начало года, D
Сумма процентных денег, I
Сумма погашения основного долга, R
Годовая срочная уплата Y
11. Ипотечный кредит выдан на 20 лет, размер кредита – (200000+1000n) руб., ставка – 6% годовых. Погашение будет происходить ежемесячно равными срочными уплатами по 1000 руб. Рассчитайте размер «шарового платежа».
D = 200000+1000 19 = 219000 руб.
Размер шарового платежа В найдем по следующей формуле:
Так как ха год будет выплачено 12000 руб.
Ответ: размер «шарового платежа» равен 25368,73 руб.
12. Сумма ипотечного долга – 10000019 = 190000 руб. Срок погашения 20 лет (240 месяцев) разбит на два период продолжительностью: 1-й период m=60 месяцев; 2-й период n = 180 месяцев. Процентная ставка – 6% годовых (проценты сложные). Погашение кредита производится ежемесячно. По условиям контракта ежегодный прирост срочных уплат 5% в первом периоде. Во втором периоде погашение производится равными срочными уплатами. Составьте план погашения кредита, используя стандартную программу Excel.
D = 190 тыс. руб., N = 240 месяцев; m = 60 месяцев
N = 180 месяцев; i = 0,06.
0,005 (месячная вставка);
Tемп роста ежемесячных расходов g = 1,051,0041.
= 190: (59,7+111,52)=1,11 тыс. руб.
Ежемесячные расходы в первом периоде:
Yt = Y1GИли Yt = 1,111,0041
Месячный расход в конце первого периода;
Y60 = 1,111,00411,41 тыс. руб.
По условиям кредита эта же сумма выплачивается ежемесячно во втором периоде. Остаток задолженности в любом месяце второго периода рассчитываем по следующей формуле:
Где Dk – остаток задолженности в месяце k;
N – число месяцев во втором периоде;
K – номер месяца во тором периоде: k = 1,2,3 (n-1);
D – остаток задолженности в первом месяце второго периода.
Составим план погашения долга
Остаток долга на начало месяца D
Процентные платежи, I
Сумма погашения основного долга R
Ежемесячные срочные уплаты
13. Размер ипотечного кредита D = (100000+1000n) руб. Срок ипотеки – 10 лет Заемщик открывает специальный счет на сумму D/10 руб., на который начисляются ежемесячно проценты по ставке 12 % годовых. Списание средств со счета идет ежемесячно в течение двух лет, сумма списаний ежемесячно уменьшается на 2 %. Ставка за кредит – 6% годовых. Разработайте график помесячного погашения задолженности, используя программу Excel.
Размер ежемесячных взносов, которые получает кредитор:
R = 1,32114 тыс. руб.
Первая сумма списания со счета:
Сумма списания со счета через t-месяцев:
Таким образом, суммы списания составят, тыс. руб.
Списания со счета, V
Взносы должника, R
Размер ежемесячных взносов, которые получает кредитор, R
14. Рассматриваются предложения двух фирм по строительству промышленного объекта:
Условия фирмы А
Условия фирмы Б
Цена нового объекта, руб.
Срок строительства, лет
Авансовые платежи (вносятся при подписании контракта), руб.
Срок кредита, лет
Льготный период, лет
Кредит погашается равными годовыми выплатами. Ставка сравнения – q = 12%. Найти современные величины всех платежей по фирме А и Б.
Найдем современную стоимость всех платежей по фирме А. Рентные платежи выплачиваются в течение 6 лет. Тогда:
Найдем современную величину всех платежей по фирме В. Срок аннуитета равен 7 – 3 = 4 года. Тогда:
Таким образом, из расчетов видно, что современная величина всех платежей по фирме А равна 639847 руб., а современная величина всех платежей фирмы В – 728014 руб. Преимущество фирмы А при принятой для сравнения процентной ставке 12% очевидно.
15. Оцените облигацию номиналом в (100+10n) руб. купонной ставкой 16%, выпущенной сроком на восемь лет, в начале жизни, в середине, за один год до погашения при значениях среднерыночной ставки 12 и 18%. Результаты обоснуйте. СТР. 82
N = 100+1019 = 290 руб.
Оценим облигацию в начале жизни, используя следующую формулу:
Где С – размер купона;
N – номинал облигации;
R – процентная ставка;
N – срок до погашения облигации
= 46,44,968 + 2900,4039 = 230,5+117,1=347,6 руб.
В середине жизни рыночная цена облигации:
= 140,9+184,3= 325,2 руб.
=124,8+149,6 = 274,4 руб.
За один год до погашения:
= 41,4 +258,9= 300,3руб.
=39,3+245,8= 285,1 руб.
Ответ: если купонная ставка меньше среднерыночной ставки, то рыночная цена облигации будет выше номинала, она будет продаваться с премией. При приближении даты выкупа стоимость облигации понижается. Обусловлено это тем, что по ней уже выплачена большая часть доходов, и к моменту выкупа остается получить только ее номинальную стоимость. Если купонная ставка больше среднерыночной, то рыночная цена облигации будет ниже номинала, в этом случае говорят, что облигация продается с дисконтом. С приближением даты выкупа происходит погашение дисконта. К концу срока погашения оценка облигации стремится к номиналу.
16. Купонную облигацию, срок жизни которой пять лет, с купоном в 10% и номиналом (1000+100n) руб. приобрели по цене (900+100n) руб. Найдите доходность к погашению.
N = 1000+10019 = 2900 руб
P =900+10019 =2800 руб.
Доходность облигации определим с помощью следующей формулы:
Где i – доходность к погашению;
Q - купонная ставка;
N – номинал облигации
Р – рыночная стоимость
N – срок до погашения облигации
Ответ: доходность к погашению равна 10,88%
17. 10% - ю купонную облигацию номиналом в N = (100+10n) руб. приобрели за 10 руб. Облигация имеет фонд погашения со следующим расписанием: 20% эмиссии после первого года, 30% - после второго года и оставшуюся часть эмиссии – после трех лет. Определите доходность к эквивалентной жизни.
Средняя жизнь облигации составит:
AL = 0,21 + 0,32 + 0,53 = 2,3 года
Рассчитаем доходность данной облигации. Заполним таблицу:
Купонная выплата, руб.
Общий денежный поток у инвесторов, руб.
Рыночная цена облигации – 10 руб. Определим доходность, продисконтировав денежный поток у инвесторов на момент выпуска облигации:
Решением этого уравнения является ставка 493 %
18. Оцените акцию, которая за первый год принесет (100+10n) руб. дивидендов, а темп прироста дивидендов составит 5% в год. Минимальная приемлемая ставка – 10%.
Div = 100+1019 = 290 руб.
Курсовая стоимость акции определяется по следующей формуле:
Где Div – размер дивидендов;
G - темп прироста;
R – ставка дисконтирования
Ответ: курсовая стоимость акции 6090 руб.
19. Оцените доходность портфеля, состоящего из пяти видов ценных бумаг. Здесь q = (5+n/2)%.
1. Банк начисляет 50 рублей обыкновенного простого процента за использование 3000 рублей в течение 60 дней . Какова норма простого процента такой сделки ?
Простой процент вычисляется по формуле :
50 =i 3000* (60/365);
I = 365*50 /(3000*60) = 0,1014 (10,14%)
S = P (1+i); (50+ 3000) = 3000 (1+i); 3050 = 3000 + 3000 i; 50/3000 = i; i = 0,0167 (1,67 %) – за 60 дней (два месяца ); за год: i = 0,0167*365/60 = 0,101388 (10,14%);
В случае простого дисконта :
P = 100000 (1 – 0,035* 72/365)= 100000 *0,993 = 99300 руб.
100000 – 99300 = 700 руб.
Прологарифмируем полученное выражение :
12 lg (1+i) = lg2 ; lg2 = 0,3
Lg (1+i) = 0,0025; (1+i) = 1, 06; i = 0,06 (6%)
Можно было не делать таких сложных расчетов . В учебниках по банковскому делу и ценным бумагам прилагаются таблицы , в которых показывается будущая стоимость единицы при определенной годовой ставке через определенный период времени .
Единица удваивается через 12 лет при 6% годовых.
Эквивалентная процентная ставка:
J = (1+ i)m/n -1 =(1+ 0,05)10/3 -1;
(1+ i)m = (1+ j)n = (1 + 0,05)10
(1+ j)n = (1 + 0,05)10 = 1,6289
(1+ i)3 =1,6289; (1+ i) = 1,1768; i = 0,1768 ≈ 17,7%
По ставке сложного процента:
Будущая стоимость единицы: 1,1576
Р = 10000/1,6289 = 6139,11 руб.
Тогда: 6139,11*1,1576 = 7139,63 руб.
500 000 = R *[(1+0,015 )4*5 -1] /0,015 * (1 + 0,015);
(1,34685-1)/0,015* 1,015 = 23,47044;
Отсюда: R = 500000/ 23,47044= 21303,4 руб.
По формуле обыкновенного общего аннуитета:
S = 500 * ((1+0,04)5*1 -1)/ ((1+ 0,04)1/4 -1 ) = 500* 0,2167/0,00985 = 11 000 руб.
Вечная рента – это аннуитет, платежи которого продолжаются в течение неограниченного времени
Эквивалентная процентная ставка равна:
J =(1+i)m/p -1 = (1+ 0,03)4/12 -1= 1,0108 -1 = 0,0108
А =R/j = 1500/0,0108 = 138888,88 руб.
Доход по облигации представляет собой поток периодических платежей в конце каждого года (простой аннуитет) и разовую выплату в конце всего срока действия облигации.
Ежегодные выплаты: R = 5000 руб., i =0,03
Р = 5000* [ 1-(1+0,03)-15]/0,03 + 100000 (1+0,03)-15 = 5000 *(1-1/1,5580)/0,03 + 100000(1/1,0315) = 5000 * 11,9384 + 100000*0,64185 = 123877 руб.
Рассчитаем будущюю стоимость 20000 рублей через 3 года, под 17% годовых.
FV = 20000 * (1 + 0,17)3 = 32032 рубля.
Ответ. Получить 35000 рублей через 3 года является более выгодным решением, при данном значении процентной ставки.
Преобразуем формулу к следующему виду:
(1 + r)n = FV / PV и подставим значения;
1,14n = 20000 / 1000 = 20, отсюда n = log 1,14 20 = 22,86 года.
Ответ. 1000 рублей нарастится до 20000 рублей при 14% годовой ставке за 22,86 года.
При расчете числа лет необходимо учитывать, что в формуле подразумевается целое число лет и цифры, рассчитываемые после запятой, имеют приблизительные значения, характеризующие близость к целому значению лет.
Преобразуем формулу к следующему виду:
R = (FV / PV)1/n - 1 и подставим значения;
R = (30 000 / 10 000)1/5 - 1;
R = 0,24573 или 24,573 %.
Ответ. 10 000 рублей нарастятся до 30 000 рублей за 5 лет при ставке ссудного процента 24,573%
K’ = K + I = 4000+44=4044,
где K – капитал или заем, за использование которого заемщик выплачивает определенный процент;
I – процентный платеж или доход, получаемый кредитором от заемщика за пользование денежной ссудой;
P – процентная ставка, показывающая сколько д. е. должен заплатить заемщик за пользование 100 ед. капитала в определенном периоде времени (за год);
D – время, выраженное в днях.
360 – число дней в году.
Время t = 80/360 = 2/9.
K’ = K + K×i×t = 4000(1 + 0.05×2/9) = 4044,
Где i – процентная ставка, выраженная в долях единицы,
T – время, выраженное в годах.
14. Величина предоставленного потребительского кредита – 6000 д. е., процентная ставка – 10% годовых, срок погашения – 6 месяцев. Найти величину ежемесячной выплаты (кредит выплачивается равными долями).
Таблица - План погашения кредита (амортизационный план)
Объяснение к таблице
Месячная выплата основного долга составит:
K / m = 6000/6 = 1000.
Месячный взнос представляет собой сумму выплаты основного долга и процентного платежа для данного месяца.
Процентные платежи вычисляются по формуле:
Где I1 – величина процентного платежа в первом месяце;
P – годовая процентная ставка, %.
Общая величина выплат за пользование предоставленным кредитом:
Общая величина ежемесячных взносов:
Так как нам известна номинальная величина векселя, дисконт, находим по формуле:
Где Kn – номинальная величина векселя;
D – число дней от момента дисконтирования до даты погашения векселя;
D – процентный ключ или дивизор (D = 3600/p = 36000/8 = 4500).
Дисконтированная величина векселя равна разности номинальной стоимости векселя и дисконта (процентного платежа):
20000 – 409 = 19591.
16. Пусть в банк вложено 20000 д. е. под 10% (D) годовых. Найти конечную сумму капитала, если расчетный период составляет: а) 3 месяца; б) 1 месяц.
При декурсивном (d)расчете сложных процентов:
Kmn = K×Ip/mmn, Ip/m = 1 + p/(100×m),
Где Kmn – конечная стоимость капитала через N лет при p% годовых и капитализации, проводимой M раз в год.
А) K = 20000×I2.54 = 20000×(1 + 10/(100×4))4 = 20000×1.104 = 22076 д. е.
Б) K = 20000×I10/1212 = 20000×(1 + 10/(100×12))12 = 20000×1.105 = 22094 д. е.
При антисипативном (a) способе расчета сложных процентов:
Kmn = K×Iq/mmn, Iq/m = 100m/(100m - q),
Где q – годовой прцент.
А) K = 20000×(100×4/(100×4 – 10))4 = 20000×1.107 = 22132 д. е.
Б) K = 20000×(100×12/(100×12 – 10))12 = 20000×1.106 = 22132 д. е.
Сначала для годовой процентной ставки 8% определим процентную уравнивающую ставку:
Затем полученную уравнивающую ставку поместим в следующую формулу:
Svmn = u× , где rk = 1 + pk/100,
Где v – число вкладов в расчетном периоде,
m – число капитализаций в год.
Rk = 1 + 1.9427/100 = 1.0194
S4×10 = 500× = 500×60.8157 = 30407.84 д. е.
U1 = u×I2%4 / III2% = 2000×1.0824 / 4.204 = 514.93 д. е.
Snm = 514.93×III2%3×4 + 2000 = 514.93×13.6803 + 2000 =
= 9044.41 д. е.
K0 = Kn×r-n = Kn×II8%20 = Kn×(1 + p/100)-n = 200000×(1 + 8/100)-20 =
= 200000×0.21454 = 42909 д. е.,
Где r = (1 + p/100) – сложный декурсивный коэффициент.
22. Найти текущую стоимость суммы 10 вкладов Постнумерандо по 5000 д. е. при 8% годовых, если капитализация осуществляется каждые полгода.
При ежегодной капитализации:
C0 = a×IVpn = 5000×IV8%10 = 5000×6.71=33550
Таблица - План погашения займа (амортизационный план)
Пояснения к таблице
Аннуитет вычисляем по формуле:
A = K×Vpn = 20000×V2%10 = 20000×0.1113 = 2226.53 д. е.
Чтобы определить выплату задолженности b1, вычисляем величину процентного платежа I:
I1 = K1×p/100 = 20000×2/100 = 400 д. е.
Выплата задолженности представляет собой разницу между аннуитетом и процентным платежом:
B1 = a – I1 = 2226.53 – 400 = 1826.53 д. е.
Таким образом, после первого года долг сократится на 1826.53 д. е. Остаток долга равен:
K2 = 20000 - 1826.53 = 18173.47 д. е.
Вычислим процентный платеж на остаток долга:
I2 = 18173.47×2/100 = 363.47 д. е.
Вторая выплата составит:
B2 = a – I2 = 2226.53 – 363.47 = 1863.06 д. е.
Долг уменьшится на величину 1863.06, остаток долга составит:
K3 = 18173.47 – 1863.06 = 16310.41 д. е.
I3 = 16310.41×2/100 = 326.21 д. е.
Третья выплата задолженности составит:
B3 = a – I3 = 2226.53 – 326.21 = 1900.32 д. е.
Вывод формулы для простой ставки процентов:
Ответ: простая ставка процентов равна 180%.
25. Кредит в размере 15 000 руб. выдан с 26.03 по 18.10 под простые 24% годовых. Определить размеры долга для различных вариантов начисления процентов.
1) «английская практика»: Т=365 или 366 дней.
2) «французская практика»: T=360 дней.
3) «германская практика»: T=360 дней.
Ответ: размер долга составляет:
- согласно «английской практике»: 17 031,781 руб.;
- согласно «французской практике»: 17 060 руб.;
- согласно «английской практике»: 17 020 руб.
26. Банк объявил следующие условия выдачи ссуды на год: за I квартал ссудный процент 24%, а в каждом последующем квартале процентная ставка по ссуде увеличивается на 3%. Определить сумму к возврату в банк, если ссуда выдана на год и составляет 15 000 руб.(простые проценты)
T = 1 год = 360 дней PV = 15 000 руб. 30×3 = 90 дней
Сумма начисленных процентов:
Сумма к возврату:
Ответ: сумма к возврату в банк составит 19 275 руб.
PV = 15 000 руб. N = 2 года J = 16% = 0,16 M = 2
Сумма на счёте клиента к концу срока:
Ответ: сумма на счёте клиента к концу срока составит 20 407,334 руб.
FV = 19 000 руб. T = 1 год = 360 дней T = 60 дней N = 1 год D = 60% = 0,6
Сумма, полученная владельцем векселя:
PV = FV – D ;
PV = 19 000 – 1 900 = 17 100 (руб.)
- величина дисконта равна 1 900 руб.;
- сумма, полученная владельцем векселя, равна 17 100 руб.
Эквивалентная годовая учётная ставка:
Ответ: эквивалентная годовая учётная ставка равна 19,4%.
Решение: FV = 19 000 руб. j = 16% = 0,16, m = 4, n = 1,5 года = года.
Ответ: сумма вклада равна 15 015,976 руб.
Решение: N = 1 год
1) M = 4, J =24% = 0,24
2) M = 2, J =26% = 0,26
3) M = 12, J = 20% = 0,2
Эффективная процентная ставка:
при N=1 год: ;
Ответ: выдача кредитов под 26% годовых с полугодовым начислением процентов банку выгоднее, т. к. эффективная годовая процентная ставка в этом случае больше (сумма кредита возрастает на 27,7% за год).
32. Банк выдаёт кредит под 24% Годовых. Полугодовой уровень инфляции составил 3%. Определить реальную годовую ставку процентов с учётом инфляции.
Решение: n = 1 год i = 24% = 0,24 = 3% = 0,03 N = 2
Реальная годовая процентная ставка:
Ответ: реальная годовая ставка процентов равна 16,9%.
Решение: = 3% = 0,03 n = 1 = 10% = 0,1
Вывод формулы для процентной ставки:
Ответ: нужно назначить ставку процентов по вкладам, равную 13,3%.
Решение: N = 12 месяцев
Ответ: уровень инфляции за год равен 42,6%.
Решение: PV = 15 000 руб. j = 72% = 0,72 m = 12 месяцев n = 6/12 года p = 3% = 0,03,
Реальная покупательная способность вклада через определённое время:
Реальный доход вкладчика:
Ответ: реальный доход вкладчика равен 2 819,811 руб.
36. Договор аренды имущества заключён на 5 лет. Аренда уплачивается суммами S1=19 000 руб., S2=20 000 руб., S3=21 000 руб. в конце 1-го, 3-го и 5-го годов. По новому графику платежей вносится две суммы: S4=22 000 руб. в конце 2-го года и S5 в конце 4-го года. Ставка банковского процента 5%. Определить S5.
Суммы платежей,
S1=19 000 S4 =22 000 S2=20 000 S5 - ? S3=21 000 руб.
0 1 2 3 4 5 Сроки платежей,
наращение дисконтирование
На рис. отмечены: Полужирным шрифтом – исходный график платежей, Курсивом – новый график платежей. Моментом приведения выбран год, совпадающий с годом платежа суммы : 4 года.
Уравнение эквивалентности: графики платежей будут эквивалентны, если сумма приведённых на какую-либо дату (на момент приведения) платежей одного графика будет равна сумме платежей другого графика, приведённых на ту же дату при неизменной ставке процентов:
Коэффициент приведения (наращения или дисконтирования):
Где: N – число лет до момента приведения:
N = N0 – Ni,
Где: Ni - срок I-го платежа.
При - коэффициент наращения;
При - коэффициент дисконтирования;
Ответ: сумма второго платежа по новому графику платежей равна 38 739,875 руб.
Решение: i = 5% = 0,05 n = 6 лет FVA = 19 000 000 руб.
Размер ежегодных платежей:
Ответ: размер ежегодных платежей равен 2 793 331,894 руб.
Решение: R = 19 000 руб. N = 2 года I = 5% = 0,05
Величина будущего фонда:
Ответ: величина будущего фонда равна 38 950 руб.
Решение: R = 1 800 руб. j = 48% = 0,48 m = 12 n = 1 год
Авансовая приведённая сумма аренды:
Ответ: равноценный платёж, взимаемый за год вперёд, равен 17 568,858 руб.
40. Двухлетняя облигация номиналом 1 000 руб. имеет 4 Полугодовых купона доходностью 20% годовых каждый. Рассчитать цену её первоначального размещения, приняв ставку сравнения 16%.
Решение: N = 2 года N = 1 000 руб. M = 2 J = 16% = 0,16 Q = 20%
Цена первоначального размещения облигации:
Ответ: цена первоначального размещения облигации равна 1 066,243 руб.
Решение: дней Т = 360 дней
1) доходность по схеме простых процентов:
2) доходность по схеме сложных процентов:
- доходность по схеме простых процентов равна 180%;
- доходность по схеме сложных процентов равна 342,1%.
Решение: I = 5% = 0,05 N = 5 лет PVA = 1 500 000 руб.
Экономические задачи ввели в единый государственный экзамен по математике (профильный уровень) с 2015 года. При их решении у экзаменующихся часто возникают затруднения, ведь в жизни они пока не сталкивались с кредитами и вкладами, а значит, плохо понимают условия задач и действия, выполняемые внутри них.
Разбор типовых задач (задание 17) из ЕГЭ по математике профильного уровня будет полезен не только выпускникам школ, но и любителям прикладных методов в банковской сфере.
Как решать экономические задачи?
Часть экономических задач можно решить универсальным способом — с помощью составления таблицы, которая позволит упорядочить данные по временным интервалам.
Для всех типов задач при составлении таблицы используется единый алгоритм.

Условия задач взяты с сайта РЕШУ ЕГЭ .
Задачи на равные платежи по кредиту
В задачах этого типа заёмщик всегда вносит равные суммы. При решении подобных задач надо следовать ряду советов.
-
Не торопитесь сразу в ходе решения использовать числовые данные задачи. Решите задачу в общем виде.
Задача 1. Рассчитываем общую сумму кредита
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
-
каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;
Какая сумма была взята в банке, если известно, что кредит был полностью погашен тремя равными платежами (то есть за три года)?
S руб. — сумма кредита,
р = 0,31,
r = 131,
В = 69 690 821 руб. — ежегодная выплата.
| Долг с начисленными процентами | Выплата | Остаток долга | |
| 1 | S * r | B | S * r — B |
| 2 | (S * r — B) * r | B | (S * r — B) * r — B |
| 3 | ((S * r — B) * r — B) * r | B | 0 |
По последней строке составляем уравнение:

Далее последовательно раскроем скобки:

Теперь можно подставить числовые данные:

Многолетняя практика по решению реальных экзаменационных вариантов показывает, что числовые данные для задач подбираются неслучайно. Составители могут специально подбирать значения таким образом, чтобы получающиеся при вычислениях дроби можно было сократить. Поэтому, прежде чем взяться за вычисление знаменателя, надо проверить, будет ли число 69 690 821 делиться на 1,31.

Ответ: Общая сумма кредита 124 809 100 руб.
Задача 2. Рассчитываем процент кредита
31 декабря 2020 г. Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на х%), затем Пётр переводит очередной платёж. Если он будет платить каждый год по 2 592 000 руб., то выплатит долг за четыре года. Если по 4 392 000 руб., то за два года. Под какой процент Пётр взял деньги в банке?
S тыс. руб. — сумма кредита,
Х% — в десятичной дроби,
r = 1 + a,
А = 2 592 000 руб. — ежегодный платёж 1,
В = 4 392 000 руб. — ежегодный платёж 2.
| Долг с начисленными процентами | Выплата | Остаток долга | |
| 1 | S * r | А | S * r — А |
| 2 | (S * r — А) * r | А | (S * r — А) * r — А |
| 3 | ((S * r — А) * r — А) * r | А | ((S * r — А) * r — А) * r — А |
| 4 | (((S * r — А) * r — А) * r — A) * r | А | 0 |
| 1 | S * r | B | S * r — B |
| 2 | (S * r — B) * r | B | 0 |
Из таблицы видно, что последнее начисление банка при каждой схеме выплат равно ежегодной выплате.
Получаем систему уравнений:

Помните о культуре вычислений и об отсутствии калькулятора.
Выражаем S из каждого уравнения:


Теперь подставляем числовые значения:

Значит, а = 1,2 — 1 = 0,2, или 20%
Ответ: Пётр взял кредит под 20%.
О чём необходимо помнить при решении экономических задач
Старайтесь предварительно упрощать выражения, используя алгебраические преобразования.
Мы разобрали алгоритм решения задач с использованием таблицы, но возможны и другие способы решений.
Еженедельная рассылка с лучшими материалами «Открытого журнала»
Без минимальной суммы, платы за обслуживание и скрытых комиссий
Для оформления продукта необходим брокерский счёт
проект «Открытие Инвестиции»
Открыть брокерский счёт
Тренировка на учебном счёте
Об «Открытие Инвестиции»
Москва, ул. Летниковская,
д. 2, стр. 4
8 800 500 99 66
Согласие на обработку персональных данных
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Автор статьи

Читайте также:

