Сколько млн рублей составила общая сумма выплат после погашения кредита
Обновлено: 24.04.2024
Задача 17 – одна из сложных задач ЕГЭ. Они делятся на “экономические” и “неэкономические”. В первых, как правило, нужно уметь определять срок кредитования, сумму кредита, банковский процент или величину платежа.
Задача 1. В июле планируется взять кредит в банке на сумму 6 млн рублей на некоторый срок.
Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил 1,8 млн рублей?
Снова мы столкнулись с условием, когда долг должен быть меньше долга на предыдущий период времени на одну и ту же величину. Это означает, что платежи не будут равными, потому что в каждый из платежей необходимо выплатить все проценты, начисленные банком до того, и еще часть суммы самого кредита. Поэтому при такой схеме первый платеж является самым крупным (проценты начисляются на целую, еще не уменьшенную нами, сумму кредита), а последний – самым маленьким.
В нашем случае процент известен, поэтому в первый платеж надо будет выплатить процент: $X \cdot \frac= 6 \cdot \frac$, да еще неизвестную часть кредита: $\frac=\frac$, и по условию эта сумма не должна быть больше 1,8 млн. Поэтому
Задача 2. В июле планируется взять кредит в банке на сумму 20 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 47 млн рублей?
Задача с похожим условием. Давайте разбираться. Как мы выяснили ранее (например, в предыдущей задаче), платежи равными не будут. Самый большой платеж – первый, а потом каждый последующий все меньше и меньше, потому что с каждым платежом долг уменьшается на одну и ту же величину и процент, следовательно, тоже.
Сначала банк начислит нам процент на всю сумму кредита: $X \cdot \frac$, но в первый же платеж мы выплатим все эти деньги и вернем еще и часть долга, равную $\frac$. Тогда мы останемся должны $X-\frac=\frac$, и уже на эту сумму банк нам начислит проценты. И так далее: выплачиваем проценты и часть долга, банк начисляет проценты на оставшуюся часть.
Тогда в конце концов мы выплатим банку весь долг – 20 млн – и всю сумму процентов, всего – 47 млн, а сумма процентов будет ни что иное, как арифметическая прогрессия:
Членов у такой прогрессии ровно столько, на сколько лет (ну или месяцев – где как) взят кредит, разность такой прогрессии равна $d=-\frac$, первый член – полная сумма, взятая в долг. Сумма арифметической прогрессии в скобках равна
В нашем случае сумма процентов равна $47-20=27$ млн, поэтому
Задача 3. В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 40 млн рублей?
Задача точно такая же, но с другими цифрами. Формулу больше не выводим, а просто ею пользуемся. Переплата равна:
Задача 4. В июле планируется взять кредит в банке на сумму 1 300 000 рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
На какое минимально количество лет можно взять кредит при условии, что ежегодные выплаты были не более 350 000 рублей?
Если бы не проценты, мы вернули бы банку долг приблизительно за 4 года: $ \frac=3,7$ . Самая большая сумма процентов – первая – равна $P=0,1\cdot1300000=130000$, остальные будут меньше. Тогда, если умножить эту сумму на 4, получим, что проценты (по максимуму) составят $4\cdot130000=520000$. Так как
то за пять лет точно справимся (помним, что проценты будут меньше с каждым платежом, сумма в 520000 сильно завышена).
Можно решать задачу по-иному, а именно, табличным способом. Необходимо просто рассчитать все платежи и начисления.
Первый год: начисляем проценты.
Второй год. Начисляем проценты:
Третий год. Начисляем проценты:
Четвертый год. Начисляем проценты:
Таким образом, выплата пятого года оказывается последней.
Задача 5. 1 января 2015 года Александр Сергеевич взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая: 1-го числа каждого месяца банк начисляет 1 % на оставшуюся сумму долга (то есть увеличивает долг на 1 %), затем Александр Сергеевич переводит в банк платеж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?
Самый большой платеж – первый – равен сумме процентов $X \cdot \frac= 1 100 000 \cdot \frac$ и части долга¸ равной $\frac=\frac$, и по условию эта сумма не должна быть больше 275 000. Поэтому
$$1 100 000 \cdot \frac +\frac=275 000$$
Иными словами, Александр Сергеевич не сможет расплатиться за 4 месяца, поэтому минимальный срок – 5 месяцев.
Задачу можно решать и так: $275 000 \cdot n=1 100 000$ – то есть $n=4$ при условии, что не надо выплачивать проценты. Наибольшую сумму процентов – $X \cdot \frac= 1 100 000 \cdot \frac=11 000$ – Александру Сергеевичу предстоит выплатить в первый платеж, потом они будут уже меньше. То есть максимальная сумма выплат (без учета того, что проценты уменьшаются, то есть с лихвой) равна $1 100 000 + 11 000\cdot 5=1 155 000$, а $275 000 \cdot 5=1 375 000$ – то есть за 5 месяцев он всяко сможет расплатиться.
Ответ: 5 месяцев
Всем здравствуйте! Меня зовут Александр. Я - профессиональный репетитор по математике, информатике, программированию, базам данных и алгоритмам. Если коротко, то я - матерый технарь.
Одно из генеральных моих направлений - подготовка школьников к успешной сдаче ЕГЭ по математике и информатике. Потратьте буквально $2-3$ минуты собственного времени и познакомьтесь с отзывами моих учеников. Средний балл моих подопечных на официальном экзамене ЕГЭ составляет $91.35$ из $100$ возможных.
Задачи на дифференцированные платежи из ЕГЭ по математике являются одними из моих любимых. Вообще задания из экономического блока мне кажутся очень интересными и познавательными. Поэтому на своих индивидуальных уроках я с большим удовольствием показываю своим ученикам различные эффективные методики их решения.
Существует по-настоящему лишь $2$ способа подготовки на высоченный итоговый балл ЕГЭ по математике:
Под началом профессионального репетитора.
Мой контактный номер телефона прописан в шапке данного сайта. Звоните, договаривайтесь о времени проведения и записывайтесь на первый пробный урок.
Условие задачи
В июле планируется взять кредит в банке на сумму \(28\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(25\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит \(9\) миллионов рублей?
Решение задачи
Это классическая задача на дифференцированные платежи из ЕГЭ по математике. Почему я так решил? Потому, что есть фраза-маркер, в которой четко дают понять, что размер займа уменьшается равномерно. Вот эта фраза: "В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года".
С кредитной программой мы разобрались! Это очень важный момент. Если вы спутаете тип кредитной программы, то гарантировано получите неправильный результат. Именно по этой причине я настоятельно прошу всех выучить свойства и признаки схемы дифференцированных платежей.
Кстати, напомню, что фундаментально кредитная программа бывает двух видов:
Кредит выплачивается по схеме аннуитетных платежей.
Давайте введем следующие обозначения:
| \(S\) - размер первоначального кредита | \(r\) - процентная ставка банка, выраженная в долях | \(R = 1 + r\) - для удобства расчетов |
| \(n\) - общее количество отчетных периодов | \(i\) - номер текущего отчетного периода | \(\%_\) - размер начисленных банком процентов за конкретный период |
| \(p_\) - размер платежа за конкретный период | \(P\) - общая сумма всех выплат/платежей | \(q\) - ставка банка, выраженная в процентах |
Хочется отметить следующее, что не все выше обозначенные переменные нам потребуются в процессе решении задачи. Но понимать математический смысл вы обязаны каждой из них, если, конечно, не хотите "завалить" экзамен ЕГЭ по математике.
Дальше, давайте рассмотрим под микроскопом следующую фразу: "наибольший годовой платеж составит \(9\) миллионов рублей". В этой фразе содержится наиважнейшая информация, и ваша цель - суметь ее расшифровать. Для этого нужно прекрасно понимать, как устроена математическая модель дифференцированных платежей, а также знать свойства этих платежей.
Как известно, в схеме дифференцируемых платежей самый $1$-ый платеж является наибольшим, а самый последний - наименьшим! Значит, когда говорят про наибольший платеж, нужно подразумевать самый $1$-ый платеж.
Из условия вытекает, что:
| $S = 28$, млн. руб. | $q = 25\%$ | $r = \frac = 0.25$ | $p_ = 9$, млн. руб. |
Наша задача определить $P$, то есть общий размер всех платежей/выплат!
Важно! Если вы хотите получить максимальный балл за решение задачи на дифференцированные платежи из ЕГЭ по математике, то в своем решении нужно привести вывод соответствуюей математической модели. Поэтому, если плохо знаете принцип работы этой модели - срочно идите ее изучать, зубрить.
Вспомним, что платеж за любой отчетный период формируется из размера начисленных процентов за данный период и равной части первоначального кредита:
$p_ = \%_ + \frac$ - размер $i$-го платежа.
Ранее мы выяснили, что из условия задачи нам известен размер $1$-го платежа ($i = 1$). Значит, процентная ставка банка $q$ действует на весь стартовый кредит:
$\%_ = \frac * S * r = S * r = 28 * 0.25 = 7$, млн. рублей. Тогда:
А размер $1$-го платежа нам задан, он равен $9$ млн. рублей, тогда решим следующее уравнение:
Оказывается, первоначальный кредит был взят сроком на $14$ лет. При этом все ограничения будут соблюдены. Например, самый наибольший/первый платеж составит $9$ миллионов рублей. Отлично! Идем дальше!
Обратимся к формулам математической модели дифференцируемых платежей и "достанем" наиболее важную из них, а именно формулу, которая позволяет вычислить размер всех платежей:
Подставим все известные величины в эту формулу и получим ответ. Заметьте, что в этой формуле фигурирует переменная $n$, то есть необходимо знать общее количество отчетных периодов. Ее значение мы нашли на предыдущем шаге ($n = 14$).
$P = \frac + 28 = \frac + 28 = 52.5 + 28 = 80.5$, млн.руб.
Готово! Результат получен! Да, получилось нецелое значение, но это и не главное. Хотя в большинстве случаев входные данные в задачах на дифференцированные платежи из ЕГЭ по математике подбираются так, чтобы на выходе образовывалось что-то целое.
Но у любознательных старшеклассников может появиться вполне закономерный вопрос: "А правильный ли ответ?". Очевидно, что, да! Но ведь нужны какие-то гарантии, верно.
Верификацию полученного результата можно произвести арифметическим способом. То есть вы можете пройтись по всем отчетным периодам, вычисляя соответствующие платежи, размер начисленных банком процентов и т.п.
Но на своих индивидуальных занятиях, совместно с учеником, мы проводим верификацию полученных результатов, посредством математического процессора "MS Excel". Это очень удобный и наглядный вариант проверки решения. Также, построенная таблица обладает хорошим аналитизмом, то есть, анализируя выкладки этой таблицы, становятся понятны многие тонкие моменты, связанные с выплатой кредита.

Данная великолепная таблица доказывает правильность нашего алгебраического решения.
Ответ: 80.5
Выводы
Для успешного решения задач на дифференцированные платежи из ЕГЭ по математике нужно знать назубок соответствующую математическую модель. Пока не поймете эту модель, даже не вздумайте пытаться что-то решать из подобного типа заданий.
На официальном экзамене, для получения максимального балла за экономическую задачу, в своем решении приводите, в том числе и вывод математической модели. В этом случае ни один эксперт в процессе проверки не сможет "придраться" к вашим математическим выкладкам.
Внимательно читайте условие задачи и обращайте особое внимание на фразы-маркеры. Это позволит вам выбрать наиболее эффективный способ решения и не ошибиться в выборе кредитной программы.
Решайте задания с применением алгебраического способа, а не арифметического. Хотя оба этих способа уместны, но более профессиональным и продвинутым считается именно алгебраический.
И, пожалуй, одно из главных - нужно любить математику.
Примеры условий реальных задач, встречающихся на ЕГЭ по математике
А сейчас я приведу список из нескольких задач на дифференцированные платежи из ЕГЭ по математике. Вы можете попробовать порешать их самостоятельно. Если будут трудности, то переходите по ссылке "Перейти к текстовому решению" и знакомьтесь полноценным моим решением.
Не забывайте о том, что раздел "Финансовая математика" содержит множество других типов задач: аннуитетные платежи, вклады, простые и сложные проценты, акции и т.д. Также зачастую попадаются комбинированные задачи, где происходит смешение моделей. Хотите во всем этом разбираться? Записывайтесь ко мне на частную подготовку!
Пример №1
В мае планируется взять кредит в банке на сумму \(10\) миллионов рублей на \(5\) лет.
Условия его возврата таковы:
Каждый декабрь долг возрастает на \(10\%\) по сравнению с концом предыдущего года.
С января по март каждого года необходимо выплатить часть долга.
В мае каждого года долг должен быть на одну и ту же величину меньше долга на май предыдущего года.
Сколько миллионов рублей составила общая сумма выплат после погашения банковского кредита?
Пример №2
В июле планируется взять кредит в банке на сумму \(6\) миллионов рублей на некоторый срок.
Условия его возврата таковы:
Каждый январь долг возрастает на \(20\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил \(1.8\) миллиона рублей?
Пример №3
В июле планируется взять кредит в банке на сумму \(20\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(30\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(47\) миллионов рублей?
Пример №4
В июле планируется взять кредит в банке на сумму \(16\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(25\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(38\) миллионов рублей?
Пример №5
В июле планируется взять кредит в банке на сумму \(6\) миллионов рублей на срок \(15\) лет.
Условия его возврата таковы:
Каждый январь долг возрастает на \(q\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найти \(q\), если известно, что наибольший годовой платеж по кредиту составит не более \(1.9\) миллиона рублей, а наименьший не менее \(0.5\) миллиона рублей.
Пример №6
\(15\) января планируется взять кредит в банке на \(39\) месяцев.
Условия его возврата таковы:
\(1-го\) числа каждого месяца долг возрастает на \(q\%\) по сравнению с концом предыдущего месяца.
Со \(2-го\) по \(14-е\) число месяца необходимо выплатить часть долга.
\(15-го\) числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на \(15-е\) число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на \(20\%\) больше суммы, взятой в кредит. Найдите \(q\).
Пример №7
Анатолий взял банковский кредит сроком на \(9\) лет. В конце каждого года общая сумма оставшегося долга увеличивается на \(17\%\), а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого года, подбираются так, чтобы в результате сумма долга каждый год уменьшалась равномерно, то есть на одну и ту же величину.
Сколько процентов от суммы кредита составила общая сумма, уплаченная Анатолием банку (сверх кредита)?
Пример №8
Анна взяла кредит в банке на срок \(12\) месяцев (\(1\) календарный год). В соответствии с банковским договором Анна возвращает кредит банку ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется \(q\%\) этой суммы, и своим ежемесячным платежом Анна погашает эти добавленные проценты и уменьшает сумму долга.
Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая модель называется "схемой с дифференцированными платежами"). Известно, что общая сумма, выплаченная Анной банку за весь период кредитования, оказалась на \(13\%\) больше, чем сумма, взятая ей в кредит. Найдите процентную ставку банка, то есть \(q\).
Пример №9
В июле планируется взять кредит в банке на сумму \(28\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(25\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит \(9\) миллионов рублей?
Пример №10
\(15\) января планируется взять кредит в банке на \(15\) месяцев.
Условия его возврата таковы:
\(1-го\) числа каждого месяца долг возрастает на \(1\%\) по сравнению с концом предыдущего месяца.
Со \(2-го\) по \(14-е\) число каждого месяца необходимо выплатить часть долга.
\(15-го\) числа каждого месяца долг должен быть на одну и ту же величину меньше долга на \(15-е\) число предыдущего месяца.
Известно, что восьмая выплата составила \(108\,000\) рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Все эти задачи на дифференцированные платежи из ЕГЭ по математике решаются достаточно быстро, если вы хорошо знаете, как устроена математическая модель дифференцируемых платежей. Повторю, уже, наверное, раз $10$-ый - разбирайтесь с математической моделью, и будем вам счастье.
Также, время от времени, рекомендую обращаться к этому списку заданий, так как он постоянно обновляется и дополняется, появляются новые условия, а также соответствующие мои математические разборы.
Что-то все равно осталось непонятным? Записывайтесь ко мне на частную подготовку!
Если после прочтения данного материала у вас остались какие-то вопросы, недопонимания, то это некритично, и, даже, вполне логично! Недостаточно пристально рассмотреть одно решение задачи на дифференцированные платежи из ЕГЭ по математике. Нужен комплексный подход!
Я - репетитор-практик, который на своих занятиях, уделяет львиное количество времени конкретным разборам, техникам и эффективным методикам решения. Всевозможной теории полно в глобальной сети Интернет, а экзамен ЕГЭ по математике является практическим, то есть нужно уметь решать, а не знать теоретические изыски.
Мои занятия проходят дистанционно, посредством таких программ, как "Скайп" и "AnyDesk". Подобный формат взаимодействия репетитора с учеником является очень удобным, позволяет задействовать мультимедийные технологии, а также достаточно недорог.
Я достаточно востребованный и известный репетитор по математике и информатике, поэтому, не откладывайте свое решение в долгий ящик. Действуйте прямо сейчас! И не забывайте, что количество ученических мест ограничено, поэтому, завтра свободных мест уже может и не остаться.
Приветствую! Меня зовут Александр и мне 35+ лет. Я - профессиональный репетитор по математике, информатике и программированию. Двумя словами - я матерый технарь. Сфера моих интересов - исследование математических моделей, применяемых в задачах экономического блока, встречающихся на официальном экзамене ЕГЭ по математике.
Да, я прекрасно понимаю, что вы чрезвычайно занятой человек и имеете в настоящий момент кучу неотложных дел, но, несмотря на это, я все-таки рекомендую потратить $2$ минуты собственного времени и познакомиться с отзывами учеников, прошедших подготовку под моим началом.
Экономические задачи на дифференцированные платежи - очень популярный тип задач, которые дают решать на ЕГЭ по математике. Если вы плохо понимаете, что такое схема дифференцированных платежей, но хотите в этом разбираться на первоклассном уровне, то берите в руки телефон, набирайте мой контактный номер и записывайтесь на первый пробный урок.
Мои частные уроки проходят в различных территориальных форматах: дистанционно, на моей/вашей/нейтральной территории. Но в настоящий момент времени бешеную популярность имеет удаленный формат, посредством, например, программы "Скайп". И вам рекомендую остановиться именно на этом формате. $90\%$ моих учеников предпочитают именно его. Это удобно, эффективно и недорого!
Условие задачи
В июле планируется взять кредит в банке на сумму $20$ миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на $30\%$ по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась $47$ миллионов рублей?
Решение задачи
Как бы решал и анализировал эту задачу я. Во-первых, нужно определить, какой тип кредитования здесь применяется. Фундаментально типы можно разделить на $2$ следующих: платежи идут по дифференцированной схеме, и платежи происходят по аннуитетной схеме.
В приведенном условии присутствуют маркеры, которые позволяют однозначно определить, к какому типу кредитования относится эта задача. Давайте обратимся к следующей фразе: " В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года". Все встало на свои места! Перед нами экономическая задача на дифференцированные платежи.
Если для вас данная фраза не является информирующей, значит, вы плохо знакомы с математической моделью, свойствами и признаками дифференцированных платежей. Поэтому, во-вторых, я просто строго настаиваю на том, чтобы вы потратили необходимое количество времени и внимательнейшим образом познакомились с понятием дифференцированных платежей. Даже, если имеете какое-то представление, то повторение не станет лишним.
Давайте введем следующие обозначения:
| \(S\) - размер первоначального кредита | \(r\) - процентная ставка банка, выраженная в долях | \(R = 1 + r\) - для удобства расчетов |
| \(n\) - общее количество отчетных периодов | \(i\) - номер текущего отчетного периода | \(\%_\) - размер начисленных банком процентов за конкретный период |
| \(p_\) - размер платежа за конкретный период | \(P\) - общая сумма всех выплат/платежей | \(q\) - ставка банка, выраженная в процентах |
Эти обозначения я использую практически в каждой экономической задаче на дифференцированные платежи. Это делает решения унифицированными и позволяет читателю переключаться между примерами, не теряя сути математических формул, за минимальное время.
Из условия вытекает, что:
| $S = 20$, млн. рублей | $q = 30\%$ | $r = \frac = \frac = 0.3$ | $P = 47$, млн. рублей |
Кстати, сразу бросается в глаза бешеная процентная ставка банка! Она слишком оторвана от реальности. Адекватная кредитная банковская ставка находится в районе $12 - 18\%$ годовых. Повторяю и буду повторять, что банковские займы - дело неправильное и их следует избегать.
Сейчас продемонстрирую решение, на которое мне потребовалось бы потратить не более $2$-х минут. Если бы я сдавал ЕГЭ по математике. Почему так быстро? Да потому, что здесь включается самая важная формула, которая выводилась нами, при построении математической модели дифференцированных платежей.
Кстати, вот эта формула: $P = \frac + S$. Если не узнали ее, то это плохо. Нужно срочно изучать математическую модель, используемую в решениях экономических задач на дифференцированные платежи.
А ведь, что характерно, это будет единственная формула, которая нам потребуется для оптимального решения и получения молниеносного ответа. Разве нет? Ведь в этой зависимости нам известно все, кроме переменной $n$. А эта $n$ и есть ни что иное, как искомая величина, которая выражает количество отчетных периодов или общее время кредитования.
Подставляем известные в уравнение и получаем ответ!
$47 * 2 = 6 * (n + 1) + 20 * 2$
$6 * (n + 1) = 94 - 40$
Готово! Быстро? А то! Сложно? Нет, достаточно знать лишь одну математическую зависимость и уметь решать линейные уравнения. То есть период кредитования должен составлять ровно $8$ лет, чтобы выполнились все требования и ограничения, указанные в постановке задачи.
Вроде получили ответ и все замечательно, но остается момент, связанный с тем, а правильный ли он? С высоченной вероятностью, что, да! Но я все-таки хочу провести доказательство правильности ответа через таблицу, сформированную в великолепной программе "MS Excel". Кстати, такие доказательные таблицы я получаю постоянно на своих частных уроках.

Данная таблица отражает все банковские операции, возникавшие в процессе кредитования. Ее структура очень наглядна. Четко прослеживается изменение тела взятой ссуды, также удобно анализировать размер платежа и размер начисляемых процентов. Всем рекомендую делать подобную верификацию полученного результата.
Ответ: 8.
Выводы
Пожалуй, можно сделать лишь один вывод: необходимо глубоко понимать математическую модель, применяемую в процессе решения экономических задач на дифференцированные платежи. Остальное дело техники и базовых математических знаний. Ну, надеюсь, что решать линейные уравнения каждый из вас умеет.
И повторюсь уже в который раз - изучайте до посинения математическую модель дифференцируемых платежей. Ссылку на эту статью я оставлял выше. Ну, ладно, так уж и быть, продублирую ее еще раз: математическая модель экономических задач на дифференцированный платеж.
Если будут трудности с пониманием того, как функционально работает схема дифференцируемых платежей, тогда записывайтесь ко мне на индивидуальную подготовку. На уроке мы с вами детально разберем все тонкости и краеугольные камни этой, уж не такой и простой, модели.
Примеры условий реальных задач, встречающихся на ЕГЭ по математике
В данном разделе я приведу лишь условия некоторого количества задач, которые наиболее часто встречаются на официальном экзамене ЕГЭ по математике. В каждой из задач акцентировано внимание на модели дифференцируемого платежа, и только на нем.
А ведь существует масса комбинированных финансовых задач, в процессе решения которых дифференцируемый платеж занимает лишь какую-то часть решения. Все подобные задачи я разбираю со своими учениками на индивидуальных занятиях.
Пример №1
В мае планируется взять кредит в банке на сумму \(10\) миллионов рублей на \(5\) лет.
Условия его возврата таковы:
Каждый декабрь долг возрастает на \(10\%\) по сравнению с концом предыдущего года.
С января по март каждого года необходимо выплатить часть долга.
В мае каждого года долг должен быть на одну и ту же величину меньше долга на май предыдущего года.
Сколько миллионов рублей составила общая сумма выплат после погашения банковского кредита?
Пример №2
В июле планируется взять кредит в банке на сумму \(6\) миллионов рублей на некоторый срок.
Условия его возврата таковы:
Каждый январь долг возрастает на \(20\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил \(1.8\) миллиона рублей?
Пример №3
В июле планируется взять кредит в банке на сумму \(20\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(30\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(47\) миллионов рублей?
Пример №4
В июле планируется взять кредит в банке на сумму \(16\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(25\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(38\) миллионов рублей?
Пример №5
В июле планируется взять кредит в банке на сумму \(6\) миллионов рублей на срок \(15\) лет.
Условия его возврата таковы:
Каждый январь долг возрастает на \(q\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найти \(q\), если известно, что наибольший годовой платеж по кредиту составит не более \(1.9\) миллиона рублей, а наименьший не менее \(0.5\) миллиона рублей.
Пример №6
\(15\) января планируется взять кредит в банке на \(39\) месяцев.
Условия его возврата таковы:
\(1-го\) числа каждого месяца долг возрастает на \(q\%\) по сравнению с концом предыдущего месяца.
Со \(2-го\) по \(14-е\) число месяца необходимо выплатить часть долга.
\(15-го\) числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на \(15-е\) число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на \(20\%\) больше суммы, взятой в кредит. Найдите \(q\).
Пример №7
Анатолий взял банковский кредит сроком на \(9\) лет. В конце каждого года общая сумма оставшегося долга увеличивается на \(17\%\), а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого года, подбираются так, чтобы в результате сумма долга каждый год уменьшалась равномерно, то есть на одну и ту же величину.
Сколько процентов от суммы кредита составила общая сумма, уплаченная Анатолием банку (сверх кредита)?
Пример №8
Анна взяла кредит в банке на срок \(12\) месяцев (\(1\) календарный год). В соответствии с банковским договором Анна возвращает кредит банку ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется \(q\%\) этой суммы, и своим ежемесячным платежом Анна погашает эти добавленные проценты и уменьшает сумму долга.
Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая модель называется "схемой с дифференцированными платежами"). Известно, что общая сумма, выплаченная Анной банку за весь период кредитования, оказалась на \(13\%\) больше, чем сумма, взятая ей в кредит. Найдите процентную ставку банка, то есть \(q\).
Пример №9
В июле планируется взять кредит в банке на сумму \(28\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(25\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит \(9\) миллионов рублей?
Пример №10
\(15\) января планируется взять кредит в банке на \(15\) месяцев.
Условия его возврата таковы:
\(1-го\) числа каждого месяца долг возрастает на \(1\%\) по сравнению с концом предыдущего месяца.
Со \(2-го\) по \(14-е\) число каждого месяца необходимо выплатить часть долга.
\(15-го\) числа каждого месяца долг должен быть на одну и ту же величину меньше долга на \(15-е\) число предыдущего месяца.
Известно, что восьмая выплата составила \(108\,000\) рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Не удивляйтесь, но приведенные экономические задачи на дифференцированные платежи решаются достаточно легко, если у вас присутствует детальнейшее понимание анатомии дифференцируемого платежа. Даже скажу больше, ответы на некоторые из представленных мною задач можно посчитать в уме, не прибегая к каким-либо записям и вычислениям на бумаге/компьютере.
Хотите научиться безошибочно решать подобный класс упражнений из экономического блока ЕГЭ по математике? Тогда записывайтесь ко мне на индивидуальную подготовку! Я – репетитор-практик с многолетним стажем, и главная цель моих занятий – выработать у вас навыки успешного решения экономических задач любого типа и любой сложности.
Хотите разбираться в экономических задачах на дифференцированные платежи? Тогда жду вас на уроке!
Если после прочтения данной статьи в вашей голове не все разложилось по нужным полочкам, значит, не все моменты вы уловили в процессе решения. Это не критично! Достаточно сложно стать профессиональным решателем, разбирая лишь готовые примеры. Нужно в обязательном порядке заниматься собственноручным прорешиванием.
Моя задача, как репетитора по математике, составить для вас индивидуальную программу подготовки, ориентированную на экономические задачи на дифференцированные платежи. Поэтому, если хотите стать асом в подобных задачах, то звоните мне по номеру, который опубликован в шапке данного сайта, и записывайтесь на $1$-е пробное занятие.
Я сугубо репетитор-практик, посвящающий львиную долю урока, разбору конкретных заданий. Минимум воды и максимум решений - вот мой девиз! Именно поэтому, превалирующее число моих подопечных получают высоченные баллы на официальных экзаменах ЕГЭ по математике и информатике.
И помните о том, что я достаточно востребованный репетитор, а количество учебных мест ограничено. Действуйте прямо сейчас, не откладывая принятия решения в долгий ящик.
Продолжаем цикл статей, посвящённых решению экономических задач ЕГЭ по математике профильного уровня.
Задачи для разбора взяты из реальных вариантов ЕГЭ прошлых лет, которые размещены на популярном среди школьников и учителей сайте РЕШУ ЕГЭ .
Задачи на расчёт дифференцированного платежа по кредиту
Дифференцированный платёж по кредиту — система выплат, при которой сумма основного долга уменьшается равномерно, то есть на одну и ту же величину каждый год (месяц). При этом платежи каждый год (месяц) отличаются и состоят из тела основного долга и начисленных процентов на остаток долга.
Таким образом, если кредит взят на n лет (месяцев), то сумма кредита — S денежных единиц — разделена на n равных частей, и каждый год (месяц) после платежа сумма долга уменьшается на s/n денежных единиц по сравнению с долгом на начало года (месяца).
Размер задолженности по кредиту после внесения очередного (k-го) платежа составит:
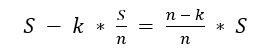
Решение задач с дифференцированными платежами по кредиту предполагает наличие у школьника базовых навыков анализа числовых данных и осуществление практических расчётов по формулам.
Задача 1. Рассчитать общую сумму выплат после полного погашения кредита
В июле планируется взять кредит в банке на сумму 14 млн руб. на некоторый срок (целое число лет). Условия его возврата таковы:
-
каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 3,85 млн руб.? Округления при вычислении платежей не производятся.
Решение
Согласно условию задачи, в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Следовательно, речь идёт о дифференцированных платежах.
Пусть кредит взят на n лет, p = 0,1 (проценты в десятичной дроби).
Ежемесячный платеж основного долга = 14/n млн руб.
Тогда основной долг по кредиту каждый июль будет составлять (в млн руб.):
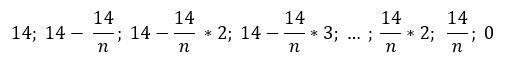
В январе каждого года начисленные проценты составят:
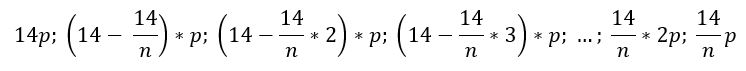
Ежегодный платёж = Сумма основного долга + Начисленные проценты
Наименьший годовой платёж — это последний платёж:
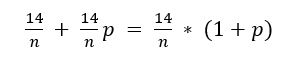
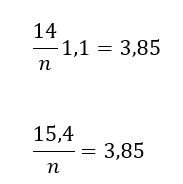
Значит, всего будет выплачено за 4 года:
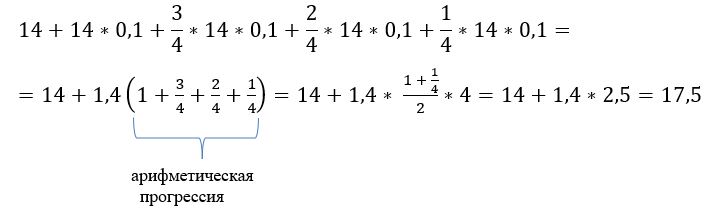
Ответ: 17,5 млн руб.
Задача 2. Рассчитать, на сколько лет взят кредит, если известна общая сумма выплат после его погашения
В июле планируется взять кредит в банке на сумму 14 млн руб. на некоторый срок (целое число лет). Условия его возврата таковы:
-
каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
На сколько лет взят кредит, если известно, что общая сумма выплат после его погашения равнялась 24,5 млн руб.?
Решение
Рассмотрим оформление решения задачи с использованием таблицы.
Пусть кредит взят на n лет.
Годовой процент равен 25%, значит, каждый год долг увеличивается в 1/4 раза.


Из условия задачи следует, что сумма выплаченных процентов составит 24,5 – 14 = 10,5 млн руб.
Следовательно, имеем уравнение:

Ответ: 5 лет.
Что необходимо учитывать при выполнении заданий ЕГЭ этого типа?
При выполнении задания № 15 ЕГЭ по математике профильного уровня выделим несколько важных нюансов.
-
Наличие в задаче словосочетаний «равными частями», «долг уменьшается на одну и ту же величину» и так далее указывает на то, что речь, скорее всего, идёт именно о дифференцированном платеже.

Еженедельная рассылка с лучшими материалами «Открытого журнала»
Без минимальной суммы, платы за обслуживание и скрытых комиссий
Для оформления продукта необходим брокерский счёт
проект «Открытие Инвестиции»
Открыть брокерский счёт
Тренировка на учебном счёте
Об «Открытие Инвестиции»
Москва, ул. Летниковская,
д. 2, стр. 4
8 800 500 99 66
Согласие на обработку персональных данных
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Вывод формулы, используемой в этой статье для решения задач, смотри здесь .
В этих формулах $r$ – процент, начисляемый банком за пользование его деньгами, $n$ – срок кредита (лет или месяцев), $A$ – платеж (ежегодный или ежемесячный, но всегда один и тот же – равные платежи), $X$ – сумма, которую мы одалживаем у банка.
Задача 1. В июле планируется взять кредит на сумму 8052000 рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (то есть за 4 года)?
Итак, по условию задачи $r=20$, $n=4$, $X=8052000$.
Искать будем сумму ежегодного платежа.
Выражаем сумму платежа $A$:
Сдвигаем запятые в числителе и знаменателе для удобства:
Сокращаем дробь. Числа 20736 и 10736 оканчиваются на 36 – число, делящееся на 4, сократим на 4:
Снова есть два числа, оканчивающиеся на 84 – а это число делится на 4, значит, снова делим на 4:
Замечаем, что число 671 не делится ни на 2, ни на 3, ни на 4, ни на 5. Зато сумма цифр на четных местах в нем равна сумме цифр на нечетных – а это признак делимости на 11( 6+1=7). И у числа 1610400 видим то же самое: 1+1+4+0=6+0, значит, оно тоже делится на 11. Сокращаем дробь на 11:
Вот теперь совсем трудно, так как 61 – простое число. Остается только попробовать разделить 146400 на 61 в столбик. И действительно, делится нацело!
$$A=2400 \cdot 1296$$
Дело за малым: не ошибиться при умножении последних двух чисел!
Ответ: 3 110 400
Задача 2. В июле планируется взять кредит на сумму 4026000 рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом прошлого года.
– с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
На сколько рублей больше придется отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года) по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за 2 года)?
Нам предстоит решить эту задачу дважды: сначала найти сумму ежегодного платежа, если мы расплачиваемся за 4 года, умножить ее затем на 4 и получить полную сумму, выплачиваемую банку в этом случае. Затем найдем сумму ежегодного платежа в случае, если сможем расплатиться за 2 года, умножим на 2 и снова найдем полную сумму, только для срока в 2 года. Ну а там вычтем из большей (4 года) меньшую (2 года) и запишем результат в ответ.
Итак, по условию задачи $r=20$, $n=4$, $X=4026000$.
Искать будем сумму ежегодного платежа.
Выражаем сумму платежа $A$:
Сдвигаем запятые в числителе и знаменателе для удобства:
Сокращаем дробь. Числа 20736 и 10736 оканчиваются на 36 – число, делящееся на 4, сократим на 4:
Снова есть два числа, оканчивающиеся на 84 – а это число делится на 4, значит, снова делим на 4:
Замечаем, что число 671 не делится ни на 2, ни на 3, ни на 4, ни на 5. Зато сумма цифр на четных местах в нем равна сумме цифр на нечетных – а это признак делимости на 11( 6+1=7). И у числа 805200 видим тот же признак: разность суммы цифр на нечетных и суммы цифр на четных местах делится на 11 ($(8+5+0)-(2+0+0)=11$ – другая форма записи признака делимости на 11), значит, число 805200 делится на 11. Сокращаем дробь на 11:
Опять 61 – простое число. Пробуем разделить 73200 на 61 в столбик. И действительно, делится нацело!
$$A=1200 \cdot 1296$$
Умножаем эти два числа аккуратно в столбик.
Получим сумму платежа, равную 1 555 200. Такую сумму банк от нас ждет ежегодно в течение 4 лет. То есть всего мы выплатили бы в таком случае $4 \cdot 1 555 200=6 220 800$
Теперь все начинаем сначала, но срок уже два года. здесь расчеты будут попроще.
Выражаем сумму платежа $A$:
Сдвигаем запятые в числителе и знаменателе для удобства:
Сокращаем дробь, сначала на 4:
Окончательная сумма после умножения 2 635 200. То есть всего мы выплатили бы в таком случае $2 \cdot 2 635 200=5 270 400$
Производим сравнение полных сумм при сроке кредита 4 года и два года:
$$6 220 800-5 270 400=950 400$$
Ответ: 950 400 – на столько больше мы заплатили бы банку, если бы пользовались кредитом 4 года вместо двух.
Задача 3. В июле планируется взять кредит в банке на сумму 10 млн рублей на 5 лет. Условия его возврата таковы:
– каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Сколько млн рублей составила общая сумма выплат после погашения кредита?
Вновь воспользуемся уже известной формулой.
По условию задачи $r=10$, $n=5$, $X=10 000 000$.
Искать будем сумму ежегодного платежа, а потом умножим ее на 5 платежей, и получим общую сумму выплат.
Автор статьи

Читайте также:

