Василий взял кредит в банке на срок 15 месяцев в конце каждого месяца 20

Обновлено: 27.04.2024

I. Если суммы, возвращаемые банку, равномерно уменьшаются

Задачи о банковских кредитных операциях оказались одними из самых популярных среди задач повышенного уровня сложности, предлагаемых на ЕГЭ выпускникам средних общеобразовательных школ.

Такие задачи в зависимости от схемы возвращения долга клиента бывают, как правило, двух типов:

Тип 1.

Физическое лицо (далее - клиент) берет кредит в банке на определенный срок (на столько-то месяцев, лет, иной срок). В конце каждого месяца (года, иного срока) долг клиента увеличивается на какое-то количество процентов, а затем уменьшается на сумму, вычисленную установленным порядком и возвращенную банку в указанный срок.

Суммы, возвращаемые банку в конце каждого месяца (года, иного периода времени) подбираются таким образом, чтобы в результате долг после каждого месяца (года, иного периода времени) будет уменьшаться равномерно, т.е. на одну и ту же величину.

Такую схему выплат банку, производимых клиентом называют дифференцированной.

Тип 2.

Клиент взял кредит в банке на определенный срок (месяцев, лет, иной срок) под определенный процент годовых (месячных).

Схема выплаты кредита: по истечении 1 года (месяца) банк начисляет проценты на оставшуюся сумму долга, т.е. увеличивает долг на согласованное с клиентом число процентов, затем клиент переводит в банк фиксированную сумму, закрепленную договором.

Эту схему возвращения долга называют аннуитетной.

Договоримся:

а) расчеты будем вести в тысячах или в миллионах рублей, кратко обозначая их так: «. тыс. руб., руб., млн руб.» или в «руб.» (рублей) в зависимости от условия задачи;

б) будем называть:

кредитным периодом - период, в течение которого осуществляется поэтапное возвращение банку суммы кредита;

кредитором - субъект, который предоставляет клиенту кредит.

Обсудим задачи типа 1.

Пусть сумма кредита, выданного клиенту на n месяцев под $$r\%$$ месячных составляет К у. е. Клиент переводит банку ежемесячно некоторую сумму, которая имеет две составляющие:

первая составляющая - неизменная (фиксированная) сумма (обозначим её Ф), равная $$\frac$$ у.е.;

вторая составляющая - выплата очередной процентной ставки банка, которая равномерно уменьшается в связи с равномерным уменьшением оставшегося долга.

Итак, происходит следующее:

К началу первого месяца кредитования долг клиента составляет $$К$$ у.е. без учета процентной надбавки (далее - основной долг), долг по процентам - $$0,01r\cdot К$$ y.e.

Сумма частичного погашения кредита в первый месяц кредитования представляет собой сумму найденных результатов, т.е. $$\frac+0,01rK=K\left(\frac+0,01r\right)$$ (у.е.).

После перевода в банк указанной суммы основной долг клиента уменьшается на $$\frac$$ у.е. и становится равным $$\frac$$у.е. А долг по процентам - $$\frac$$ у.е. И такой «процесс» будет продолжаться до полного погашения основного долга клиента.

Скажем это другими словами:

- основной долг из месяца в месяц равномерно уменьшается ровно на $$\frac$$у.е.

- подобное уменьшение основного долга на постоянную сумму из-за равномерного уменьшения всего долга клиента обеспечит равномерное уменьшение и долга по процентам.

Таким образом, последовательность, составленная из процентных ставок банка, есть некоторая конечная арифметическая прогрессия $$(a_n),$$ состоящая из членов, первый член которой равен $$0,01rК$$, а последний, $$n-$$й член, равен $$\frac$$.

Знание этих двух параметров прогрессии позволяет решить почти любую задачу рассматриваемого типа без учета неизменной части очередных долгов клиента.

Далее мы так и поступим при рассмотрении задач, связанных с дифференцированной схемой начисления процентных надбавок.

Задача 1.

Сергей взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга за каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила общая сумма, уплаченная Сергеем банку (сверх кредита)?

Пусть размер кредита равен K у.е. Тогда процентная ставка банка в первом месяце кредитования составит $$a_1=0,12K=\frac$$у.е., в последний (девятый) месяц кредитования - $$a_9=0,12K:9=\frac$$ (у.е.). Cумма первых 9 членов арифметической прогрессии \[S_9=\frac\cdot 9=\left(\frac+\frac\right):2\cdot 9=\frac=0,6K.\]

Таким образом, общая сумма, уплаченная банку Сергеем, составляет $$60\%$$от суммы кредита. ($$0,6К:К\cdot 100\%=60\%)$$.

Задача 2.

Иван взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 10\%, а затем уменьшается на сумму, уплаченную Иваном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга за каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. За весь срок кредитования Иван выплатил банку в общей сложности 16~875 рублей. Какую сумму он взял в кредит? \noindent

Пусть К - сумма кредита.

Процентная ставка банка в первый месяц кредитования $$0,1К,$$ в последний (6-й месяц) $$\frac,$$ сумма всех переплат Ивана $$\left(0,1К+\frac\right):2\cdot 6=\frac\cdot 3=0,35К.$$

За весь срок кредитования Иван выплатил банку сумму, равную $$К+0,35К=1,35К$$. По условию задачи: $$1,35К=16875$$. Откуда: $$К=12500.$$

О т в е т: 12500 рублей.

Задача 3.

Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга за каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63\%. Найдите месячную процентную ставку. \noindent

Пусть К - сумма кредита, $$r-$$ месячная процентная ставка банка.

Процентная ставка банка в первый месяц кредитования $$0,01rК,$$ в последний (6-й месяц) $$\frac.$$

Сумма всех переплат Антона $$\left(0,01rК+\frac\right):2\cdot 6=\frac\cdot 3=0,035rК.$$ Из условия задачи следует: $$0,035rК=0,63К.$$ Значит, $$r=0,63K:0,035K=18.$$

Задачи, рассмотренные выше, являются самыми простыми. Рассмотрим теперь несколько задач, предложенных на ЕГЭ в 2019-м году, которые, быть может, несколько посложнее .

Задача 4.

В июле планируется взять кредит в банке на сумму 3 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:

- каждый январь долг возрастает на 20\% по сравнению с концом предыдущего года;

- с февраля по июнь каждого года необходимо выплатить часть долга;

- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платеж составит 0,24 млн рублей?

Предположим что кредит будет оформлен на $$n$$лет.

Неизменная часть выплат клиента будет равна $$\frac$$ млн руб. в год, размер процентной

надбавки в первый год кредитования составит $$3\cdot 0,2=0,6$$ млн руб., а в последний ($$n-$$й) год кредитования $$\frac$$ млн руб.

Так как выплата банку будет наименьшей именно в последний год кредитования, то сумма $$\frac+\frac$$ по условию задачи окажется равной 0,24, т.е. $$\frac=0,24$$. $$n=\frac\Leftrightarrow n=15.$$

В первый год кредитования банку будет возвращено $$\frac+0,6=0,2+0,6=0,8$$ (млн руб.) B 15-й год: 0,24 млн рублей.

О т в е т: 7,8 млн рублей.

Задача 5.

В июле планируется взять кредит в банке на срок 15 лет. Условия его возврата таковы:

- каждый январь долг возрастает на r % по сравнению с концом предыдущего года;

- с февраля по июнь каждого года необходимо выплатить часть долга;

- в июле каждого года долг должен быть на одну и ту же величину меньше долга~на~ июль предыдущего года.

Найдите r, если известно, что за весь период выплатили на 15\% больше, чем взяли в кредит.

Пусть размер планируемого кредита равен К у.е.

Неизменная часть выплат клиента будет равна $$\frac$$ у.е. в год. Размер процентной

\noindent надбавки в первый год кредитования составит $$0,01rK$$ у.е. в $$15-$$й год кредитования $$\frac$$ у.е.

Ежегодные платежи клиента по процентам образуют конечную арифметическую прогрессию, сумма первых 15 членов которой равна

$$\left(0,01rК+\frac\right):2\cdot 15=(16\cdot 0,01rК:30\cdot 15=0,08rК.$$ Полученный результат по условию задачи равен $$0,15rK.$$ $$0,08rK=0,015K<\Leftrightarrow >r=1,875.$$

Задача 6.

В июле планируется взять кредит в банке на сумму 6 млн рублей на срок 15 лет. Условия его возврата таковы:

- каждый январь долг возрастает на \% по сравнению с концом предыдущего года;

- с февраля по июнь каждого года необходимо выплатить часть долга;

- в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

Найдите если известно, что набольший платеж по кредиту составляет не более 1,9 млн рублей, а наименьший - не менее 0,5 млн. рублей.

Неизменная часть ежегодных платежей $$\frac=0,4$$ (млн.руб.) , переменная часть: в

первый год кредитования $$6\cdot 0,01r=0,06r$$ (млн руб.), в$$15-$$й год кредитования $$\frac=0,004r$$ (млн руб.)

Так как выплата банку будет наименьшей в последний год кредитования, наибольшей - в первый год, то имеет место цепочка равносильных систем верных неравенств: \[<\left\< \begin 0,4+0,06r?1,9 \\ 0,4+0,004r?0,5 \end \right.><\Leftrightarrow ><\left\< \begin 0,06r?1,5 \\ 0,004r?0,1 \end \right.>\Leftrightarrow <\left\< \begin r?25 \\ r?25 \end \right.><\Leftrightarrow >r=25.\]

Задача 7.

15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:

- 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на15-е число предыдущего месяца.

Какую сумму следует взять в кредит, чтобы общая сумма выплат после его полного погашения равнялась 1 млн рублей? (Cчитайте, что округления при вычислении платежа не производится).

Пусть сумма планируемого кредита равна$$К$$ рублей. Неизменная часть ежегодных платежей составляет $$\frac$$млн. руб. Переменная часть:

в первый год кредитования $$0,02r$$ млн руб.,

в$$15-$$й год кредитования $$\frac=\frac$$ (млн руб.)

Все платежи клиента по процентным ставкам банка образуют конечную арифметиче-скую прогрессию $$(а_)$$, у которой $$a_1=0,02К$$, $$a_=\frac$$.

Наша задача: найти сумму всех 24 членов этой прогрессии. \[S_=\frac>\cdot 24=\frac\cdot 24=0,25К.\]

Сумма выплат клиента банку в целом составит $$К+0,25К=1,25К$$ (млн. руб.) По условию задачи: $$1,25SК=1<\Leftrightarrow >К=0,8.$$ Итак, $$К=0,8$$млн. руб. = 800~000 руб.

О т в е т: 800~000 рублей.

Задача 8.

15-го апреля планируется взять в банке кредит на сумму 1 200 тысяч рублей на $$(n+1)$$ месяц.

\noindent Условия его возврата таковы:

- 1-го числа каждого месяца долг увеличивается на \% по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

-15-го числа каждого с 1-го по -й месяц долг должен быть на 80 тысяч рублей меньше долга на 15-е число предыдущего месяца;

-15-го числа -го месяца долг составит 400 тысяч рублей;

- к 15-му числу $$(n+1)$$ месяца долг должен быть погашен полностью. Найдите $$r$$, если банку всего было выплачено 1 288 тысяч рублей.

Из условия задачи следует: $$n=(1200-400):80=10.$$

Долг на 15-е число 10-го месяца фактически совпадает с долгом на начало $$11-$$го месяца.

\noindent О т в е т: 1.

Задача 9.

15-го января планируется взять в банке кредит на сумму 300 тысяч рублей на 21 месяц.

\noindent Условия его возврата таковы:

- 1-го числа каждого месяца долг увеличивается на 2 \% по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

-15-го числа каждого с 1-го по 20-й месяц долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;

-15-го числа 20-го месяца долг составит 100 тысяч рублей;

- к 15-му числу 21 месяца долг должен быть погашен полностью.

Найдите общую сумму выплат после полного погашения кредита.

Из условия задачи ясно, что 15-го числа каждого с 1-го по 20-й месяц долг должен

\noindent быть на 10 тыс. руб. меньше долга на 15-е число предыдущего месяца. $$(300-100):20=10$$ (тыс. руб.)

Долг на 15-е число 20-го месяца фактически совпадает с долгом на начало $$21-$$го месяца.

В первый месяц процентная надбавка банка составит $$300\cdot 0,02=6$$ (тыс. руб.), в 21-й месяц $$100\cdot 0,02=2$$ (тыс. руб.)

Процентные ставки банка образуют убывающую арифметическую прогрессию $$(a_n)$$, где $$a_1=300\cdot 0,02=6,а_=100\cdot 0,02=2.$$

Общая сумма платежей клиента за весь период кредитования составит: $$300+84=384$$ (тыс. руб.)

О т в е т: 384~000 рублей.

Задача 10.

15-го января планируется взять в банке кредит на 700 тысяч рублей на (+1) месяц. Условия его возврата таковы:

- 1-го числа каждого месяца долг увеличивается на 1\% по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить одним платежом часть долга;

- 15-го числа каждого с 1-го по -й месяц долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;

- за (+1)-й месяц долг должен быть погашен полностью.

Найдите , если банку всего было выплачено 755 тысяч рублей, а долг на 15-е число

\noindent -го месяца составлял 300 тысяч рублей.

Обратим внимание на то, что данная задача несколько отличается от задач, которые рассмотрены выше. Дело в том, что в последний $$(n+1)$$ - й месяц кредитования клиент будет вносить в банк большую сумму, нежели в в предыдущие месяцы кредитования.

Следовательно, в данном случае и процентная ставка банка не будет равна $$\frac$$ тыс. руб.

Переплата клиента за весь период кредитования составит $$755-700=55$$ (тыс. руб).

Процентная ставка за первый месяц кредитования равна $$700\cdot 0,01=7$$ (тыс. руб.), а за (+1)-й месяц $$300\cdot 0,01=3$$ (тыс. руб.)

Задача 11.

15 января планируется взять кредит в банке на некоторую сумму на 21 месяц. Условия его возврата таковы:

- 1-го числа каждого месяца долг увеличивается на 1\% по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить одним платежом часть долга;

- на 15-е число каждого с 1-го по 20-й месяц долг должен уменьшаться на 40 тыс. руб.

- за двадцать первый месяц долг должен быть погашен полностью.

Сколько тысяч рублей составляет долг на 15-е число 20-го месяца, если банку всего было выплачено 1852 тыс. рублей?

Пусть размер кредита составляет тыс. руб. В контексте данной задачи процентные

\noindent ставки банка будут уменьшаться по правилам арифметической прогрессии $$(а_n),$$ где

$$а_1=0,01К,n=21,$$разность $$d=-0,01\cdot 40=-0,4,$$

Процентная ставка банка за 21-й кредитный месяц равна $$a_=a_1+20d=0,01K-8.$$ А сумма процентных ставок, выплаченная банку сверх кредита, будет равна

Вся сумма, выплаченная банку, равна $$1,21K-84,$$ что в свою очередь равно 1852.

\noindent Таким образом, $$1,21K-84=1852$$ $$\Leftrightarrow $$ $$К=\frac$$ $$\Leftrightarrow $$ $$К=1600.$$

Долг на 15-е число 20-го месяца фактически совпадает с долгом клиента на начало 21-го кредитного месяца. (тыс. руб.)

Рассмотрим новую последовательность - последовательность долгов клиента перед каждым кредитным месяцем, которая является также арифметической прогрессией. Первый член ее равен 1600, разность равна 40. Нам надо найти ее 21-й член, который как было сказано выше, равен долгу на 15-е число 20-го месяца. Искомый долг равен

Задание 15 № 562008

Алексей планирует 15 декабря взять в банке кредит на 2 года в размере 1 806 000 рублей. Сотрудник банка предложил Алексею два различных варианта погашения кредита, описание которых приведено в таблице.

− Каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

−1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

− со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

− 15 числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;

На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Алексея варианту погашения кредита?

Пусть S — размер кредита, он равен 1806 тысячам рублей. Срок погашения кредита n составляет 2 года или 24 месяца. Процентная ставка r составляет в первом варианте 15% годовых, а во втором 2% ежемесячно.

В первом варианте долг х выплачен двумя платежами, поэтому откуда

Сумма выплат составляет тыс. руб.

Во втором варианте суммы долга составляют арифметическую прогрессию:

а выплаты равны

Поэтому для суммы выплат получаем:

Следовательно, более выгоден кредит, описанный в варианте 1; разность сумм выплат составит

Ответ: 35 700 рублей.

Задание 15 № 562037

Виктор планирует 15 декабря взять в банке кредит на 2 года в размере 1 962 000 рублей. Сотрудник банка предложил Виктору два различных варианта погашения кредита, описание которых приведено в таблице.

− Каждый январь долг возрастает на 18% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

−1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;

− со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Виктора варианту погашения кредита?

Пусть S — размер кредита, он равен 1962 тысячам рублей. Срок погашения кредита n составляет 2 года или 24 месяца. Процентная ставка r составляет в первом варианте 18% годовых, а во втором 2% ежемесячно.

В первом варианте долг х выплачен двумя платежами, поэтому откуда

Сумма выплат составляет тыс. руб.

Во втором варианте суммы долга составляют арифметическую прогрессию:

а выплаты равны

Поэтому для суммы выплат получаем:

Следовательно, более выгоден кредит, описанный в варианте 2; разность сумм выплат составит

Ответ: 53 820 рублей.

Аналоги к заданию № 562008: 562037 Все

Задание 15 № 562253

В январе 2005 года ставка по депозитам в банке «Фантазия» составила x% годовых, а в январе 2006 года — y% годовых, причем известно, что x + y = 30. В январе 2005 года вкладчик открыл депозитный счёт в банке «Фантазия», положив на него некоторую сумму. В январе 2006 года, по прошествии года со дня открытия счёта, вкладчик снял со счёта пятую часть этой суммы. Укажите значение x, при котором сумма на счёте вкладчика в январе 2007 года является максимально возможной.

Пусть первоначальный вклад составил тогда через год (после начисления процентов) величина вклада составит После снятия со счёта пятой части первоначальной суммы величина вклада составит Ещё через год (после начисления процентов) величина вклада составит

Наибольшее значение этого выражения достигается в той же точке, что и наибольшее значение квадратичной функции на интервале Графиком этой функции является парабола с ветвями, направленными вниз, вершина параболы равна среднему арифметическому абсцисс точек пересечения параболы с осью абсцисс: Значит, наибольшее значение на интервале достигается в точке

Задание 15 № 561179

В январе 2020 года Борис взял кредит в банке на сумму рублей. По договору с банком Борис должен был погасить долг двумя равными платежами в феврале 2021 года и феврале 2022 года, при условии, что в январе 2021 года и январе 2022 года сумма оставшегося долга увеличивается на 10%. В феврале 2021 года Борис сделал первую выплату в соответствии с договором. После этого ему удалось договориться с банком о рефинансировании кредита и уменьшить процент, на который сумма долга вырастет в январе 2022 года, до 7%. Какую сумму сэкономит Борис на рефинансировании своего кредита?

Пусть x миллионов рублей составляла ежегодная выплата по изначальному договору, тогда по условию задачи

Величина долга после первой выплаты составляет 4,2 · 1,1 − 2,42 = 2,2 миллионов рублей. Согласно условию, выгода от рефинансирования составляет 3% этой суммы, что составляет рублей.

Ответ: 66 000 рублей.

Задание 15 № 561231

В январе 2020 года Василий взял кредит в банке на сумму рублей. По договору с банком Василий должен был погасить долг двумя равными платежами в феврале 2021 года и феврале 2022 года, при условии, что в январе 2021 года и январе 2022 года сумма оставшегося долга увеличивается на 20%. В феврале 2021 года Василий сделал первую выплату в соответствии с договором. После этого ему удалось договориться с банком о рефинансировании кредита и уменьшить процент, на который сумма долга вырастет в январе 2022 года, до 16%. Какую сумму сэкономит Василий на рефинансировании своего кредита?

Пусть x миллионов рублей составляла ежегодная выплата по изначальному договору, тогда по условию задачи

Величина долга после первой выплаты составляет 3,3 · 1,2 − 2,16 = 1,8 миллионов рублей. Согласно условию, выгода от рефинансирования составляет 4% этой суммы, то есть равняется 0,04 · 1 800 000 = 72 000 рублей.

Ответ: 72 000 рублей.

Аналоги к заданию № 561179: 561231 Все

Источник: А. Ларин. Тренировочный вариант № 348., Пробный вариант ЕГЭ по математике 18.03.21 Санкт-Петербург. Вариант №2

Задание 15 № 532056

15‐го декабря 2018 года Саша и Паша взяли в банке одинаковые суммы в кредит на 12 месяцев. Банк предложил им похожие схемы погашения долга.

Условия возврата кредита у Саши оказались следующие:

— 1‐го числа каждого месяца долг возрастает на 10% по сравнению с концом предыдущего месяца;

— со 2‐го по 14‐е число месяца необходимо выплачивать одним платежом часть долга;

— на 15‐е числа каждого месяца долг должен быть на одну и ту же сумму меньше долга, чем на 15‐е число предыдущего месяца.

У Паши условия возврата кредита были таковы:

— 1‐го числа каждого месяца долг возрастает на 10% по сравнению с концом предыдущего месяца;

— со 2‐го по 14‐е число месяца необходимо выплачивать одним платежом часть долга;

— на 15‐е число каждого месяца с января по ноябрь включительно долг должен уменьшаться на 50 тыс. руб.;

— в декабре 2019 года весь оставшийся на тот момент долг должен быть полностью погашен.

Когда в декабре 2019 года Саша и Паша рассчитались со своими кредитами, выяснилось, что один из них выплатил за год банку на 429 тыс. руб. больше, нежели другой. Определите, какая сумма была взята каждым в кредит.

Пусть суммы кредитов равны S тыс. руб., повышающий коэффициент Составим таблицу по данным задачи для Саши.

Один из типов экономических задач — это задачи на платежи с равномерно убывающим долгом. Каждый месяц (период) основной долг уменьшается на одинаковую сумму. Ежемесячный платёж будет состоять из суммы основного долга и суммы начисленных процентов на остаток долга.

В этом случае мы имеем дело с дифференцированными платежами.

Внимание: в задачах этого типа применяется формула суммы n-первых членов арифметической прогрессии.

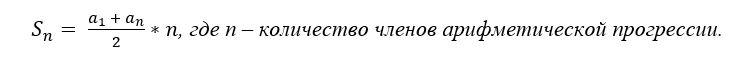
Задачи для разбора берутся из вариантов ЕГЭ прошлых лет, размещённых на популярном среди школьников и учителей сайте РЕШУ ЕГЭ .

Задача 1. Рассчитать сумму кредита

15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:

Какую сумму следует взять в кредит, чтобы общая сумма выплат по кредиту после полного его погашения составила 2 млн руб. (никакие округления при вычислении платежей не производятся)?

S тыс. руб. — сумма кредита,

2 млн руб. = 2000 тыс. руб.,

X тыс. руб. — ежемесячная выплата основного долга.

Суммы ежемесячного долга: S; (S — X); (S — 2 * X . S — 47 * X); (S — 48 * X); 0

S * p; (S — X) * p; (S — 2 * X) * p . (S — 47 * X) * p; (S — 48 * X) * p; 0

Сумма выплат = Сумма кредита + Проценты

S * (1 + 49 * p — 24 * p) = 2000

S * (1 + 25 * 0,01) = 2000

S = 1600 тыс. руб., или 1,6 млн руб.

Ответ: 1,6 млн руб.

Задача 2. Рассчитать сумму кредита

15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1,604 млн руб. (1604 тыс. руб.)?

Задача отличается от предыдущей — выплаты по основному долгу (30 тыс. руб.) осуществляются только первые 20 месяцев, а значит, в последний месяц выплата будет иной.

S тыс. руб. — сумма кредита

Суммы ежемесячного долга: S; (S — 30); (S — 60. S — 570); (S — 600); 0

Начисленные проценты: S * р; (S — 30) * р; (S — 60) * р. (S — 570) * р; (S — 600) * р; 0

Сумма выплат = Сумма кредита + Проценты

S * (1 + 21 * 0,03) — 0,03 * 6300 = 1604

1,63 * S — 189 = 1604

1,63 * S = 1604 + 189

S = 1100 тыс. руб., или 1,1 млн руб.

Ответ: 1,1 млн руб.

Задача 3. Рассчитать, на сколько месяцев планируется взять кредит

15 января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условия его выплаты таковы:

1-го числа n-ого месяца долг возрастёт на 3% по сравнению с концом предыдущего месяца;

На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?

Превышение выплат на 30% от суммы кредита — за счёт выплаченных процентов.

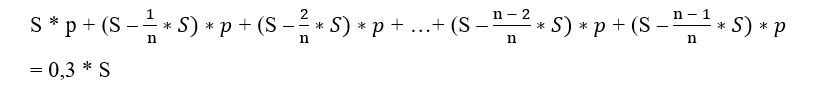
Раскрываем скобки и группируем слагаемые.

Ответ: 19 месяцев.

Еженедельная рассылка с лучшими материалами «Открытого журнала»

Без минимальной суммы, платы за обслуживание и скрытых комиссий

Для оформления продукта необходим брокерский счёт

проект «Открытие Инвестиции»

Открыть брокерский счёт

Тренировка на учебном счёте

Об «Открытие Инвестиции»

Москва, ул. Летниковская,
д. 2, стр. 4

8 800 500 99 66

Согласие на обработку персональных данных

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Экономические задачи ввели в единый государственный экзамен по математике (профильный уровень) с 2015 года. При их решении у экзаменующихся часто возникают затруднения, ведь в жизни они пока не сталкивались с кредитами и вкладами, а значит, плохо понимают условия задач и действия, выполняемые внутри них.

Разбор типовых задач (задание 17) из ЕГЭ по математике профильного уровня будет полезен не только выпускникам школ, но и любителям прикладных методов в банковской сфере.

Как решать экономические задачи?

Часть экономических задач можно решить универсальным способом — с помощью составления таблицы, которая позволит упорядочить данные по временным интервалам.

Для всех типов задач при составлении таблицы используется единый алгоритм.

Условия задач взяты с сайта РЕШУ ЕГЭ .

Задачи на равные платежи по кредиту

В задачах этого типа заёмщик всегда вносит равные суммы. При решении подобных задач надо следовать ряду советов.

Задача 1. Рассчитываем общую сумму кредита

В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

Какая сумма была взята в банке, если известно, что кредит был полностью погашен тремя равными платежами (то есть за три года)?

S руб. — сумма кредита,
р = 0,31,
r = 131,
В = 69 690 821 руб. — ежегодная выплата.

Долг с начисленными процентами	Выплата	Остаток долга
1	S * r	B	S * r — B
2	(S * r — B) * r	B	(S * r — B) * r — B
3	((S * r — B) * r — B) * r	B	0

По последней строке составляем уравнение:

Далее последовательно раскроем скобки:

Теперь можно подставить числовые данные:

Многолетняя практика по решению реальных экзаменационных вариантов показывает, что числовые данные для задач подбираются неслучайно. Составители могут специально подбирать значения таким образом, чтобы получающиеся при вычислениях дроби можно было сократить. Поэтому, прежде чем взяться за вычисление знаменателя, надо проверить, будет ли число 69 690 821 делиться на 1,31.

Ответ: Общая сумма кредита 124 809 100 руб.

Задача 2. Рассчитываем процент кредита

31 декабря 2020 г. Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на х%), затем Пётр переводит очередной платёж. Если он будет платить каждый год по 2 592 000 руб., то выплатит долг за четыре года. Если по 4 392 000 руб., то за два года. Под какой процент Пётр взял деньги в банке?

S тыс. руб. — сумма кредита,
Х% — в десятичной дроби,
r = 1 + a,
А = 2 592 000 руб. — ежегодный платёж 1,
В = 4 392 000 руб. — ежегодный платёж 2.

Долг с начисленными процентами	Выплата	Остаток долга
1	S * r	А	S * r — А
2	(S * r — А) * r	А	(S * r — А) * r — А
3	((S * r — А) * r — А) * r	А	((S * r — А) * r — А) * r — А
4	(((S * r — А) * r — А) * r — A) * r	А	0
1	S * r	B	S * r — B
2	(S * r — B) * r	B	0

Из таблицы видно, что последнее начисление банка при каждой схеме выплат равно ежегодной выплате.

Получаем систему уравнений:

Помните о культуре вычислений и об отсутствии калькулятора.

Выражаем S из каждого уравнения:

Теперь подставляем числовые значения:

Значит, а = 1,2 — 1 = 0,2, или 20%

Ответ: Пётр взял кредит под 20%.

О чём необходимо помнить при решении экономических задач

Старайтесь предварительно упрощать выражения, используя алгебраические преобразования.

Мы разобрали алгоритм решения задач с использованием таблицы, но возможны и другие способы решений.

Еженедельная рассылка с лучшими материалами «Открытого журнала»

Без минимальной суммы, платы за обслуживание и скрытых комиссий

Для оформления продукта необходим брокерский счёт

проект «Открытие Инвестиции»

Открыть брокерский счёт

Тренировка на учебном счёте

Об «Открытие Инвестиции»

Москва, ул. Летниковская,
д. 2, стр. 4

8 800 500 99 66

Согласие на обработку персональных данных

Встречаются задачи, в которых долг по кредиту уменьшается неравномерно, а убывает согласно данным, представленным в таблице.

Задачи для разбора взяты с сайта РЕШУ ЕГЭ .

Задача 1. Рассчитываем разницу между общей суммой выплат и суммой самого кредита

15 января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

При решении данной задачи воспользуемся советами, данными в прошлой статье «Проценты по кредиту с равными платежами».

Учитываем, что общая сумма выплат будет превышать сумму кредита за счёт начисленных и уплаченных процентов.

I способ — решим задачу в общем виде, приняв за сумму кредита S руб. р = 5% = 0,05,

Представим решение в виде таблицы.

Долг с начисленными процентами, руб.	Выплата, руб.	Остаток долга, руб.	Остаток долга, %
Февраль	Sr	Sr — 0,9S	0,9S	90%
Март	0,9Sr	0,9Sr — 0,8S	0,8S	80%
Апрель	0,8Sr	0,8Sr — 0,7S	0,7S	70%
Май	0,7Sr	0,7Sr — 0,6S	0,6S	60%
Июнь	0,6Sr	0,6S r — 0,5S	0,5S	50%
Июль	0,5Sr	0,5Sr	0	0%

Общая сумма выплат составит:

Общая сумма выплат от суммы кредита:

Следовательно, переплата равна 22,5%.

II способ — используем частный случай.

Пусть сумма кредита равна 100 руб.

Долг с начисленными процентами, руб.	Выплата, руб.	Остаток долга, руб.	Остаток долга, %
Февраль	100 * 1,05 = 105	105 — 90 = 15	90	90%
Март	90 * 1,05 = 94,5	94,5 — 80 = 14,5	80	80%
Апрель	80 * 1,05 = 84	84 — 70 = 14	70	70%
Май	70 * 1,05 = 73,5	73,5 — 60 = 13,5	60	60%
Июнь	60 * 1,05 = 66,3	66,3 — 50 = 13	50	50%
Июль	50 * 1,05 = 52,5	52,5	0	0%

Общая сумма выплат:

Следовательно, переплата равна 22,5%.

Задача 2. Рассчитываем наибольшее значение процентов, при котором общая сумма выплат будет меньше заданного числа

15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн руб. Условия его возврата таковы:

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн руб.

Выплата, млн руб.

Остаток долга, млн руб.

Обратите внимание! Ежемесячная выплата рассчитывается как разность между долгом на начало месяца и остатком долга. Следовательно, третий столбец заполняется в последнюю очередь.

Общая суммы выплат: