В сберегательном банке имеется два вида денежных вкладов с простым и сложным процентом
Обновлено: 26.07.2024
Употребление термина «процент» в России начинается с XVIII в. Это понятие впервые ввёл Пётр I. Однако считается, что подобные вычисления начали применяться ещё в Смутное время — как результат первой в мировой истории привязки чеканных монет 1 к 100, когда рубль сначала состоял из 10 гривенников, а позже из 100 копеек.
Долгое время под процентами понимались исключительно прибыль или убыток на каждые 100 рублей. Проценты применялись только в торговых и денежных сделках. Затем область их применения расширилась.
Например, можно услышать фразы «в выборах приняли участие 60% избирателей», «успеваемость в классе 95%», «банк начисляет 12% годовых», «молоко содержит 1,5% жира», «материал состоит из 100% хлопка», «скидка составляет 5%», «на карту начисляется кэшбэк 3,5%» и так далее.
Современная жизнь делает задачи на проценты актуальными. Вопросы инфляции, девальвации, повышения цен, снижения покупательной способности касаются каждого человека. Школьники — будущие участники финансового рынка, налогоплательщики, вкладчики, заёмщики, поэтому уже на начальных ступенях образовательной системы необходимо вводить финансовое обучение.
Вполне закономерно, что каждый из нас хочет получать дополнительный доход. Банковские вклады (депозиты) — простой способ не только сохранить, но и приумножить свои сбережения. У всех банков разные процентные ставки, которые зависят от условий хранения денег: валюты, сроков, суммы размещения, возможности снятия и пополнения счёта, капитализации процентов.
Давайте разберёмся с понятием «процентная ставка по вкладу» и видами процентов.
Процентная ставка — это процент, который клиент получает за размещение средств на вкладе на определённый срок. Обычно подразумевается годовая процентная ставка. Если срок вклада больше или меньше года, для расчёта дохода необходимо привести ставку к реальному сроку вклада.
Однако выгода банковского вклада оценивается не только по процентной ставке. Большое влияние на доходность оказывает способ начисления процентов. В финансовой сфере существует понятие простого и сложного процента.
Простые проценты начисляются по следующей формуле:
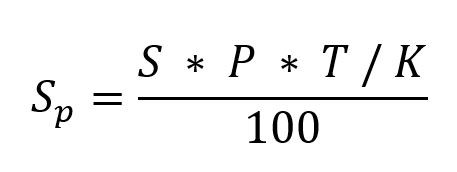
Sp — выплаченные проценты;
S — первоначальная сумма вложений;
P — годовая ставка;
T — количество дней вклада;
K — количество дней в году — 365 или 366.
Пример 1. Вкладчик размещает 1 января 2021 г. (не високосный год) вклад в размере 350 000 руб. под 4,7% годовых сроком на 9 месяцев (273 дня).
Процентный доход по данному вкладу составит:
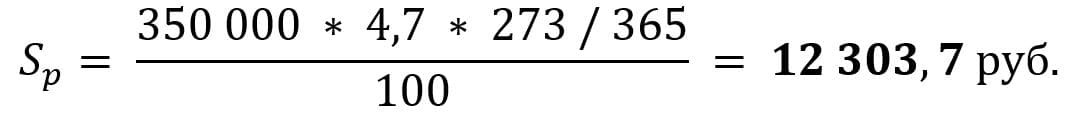
Капитализированный (причисленный) процент — процент, начисляемый на сумму вклада и сумму ранее начисленных по вкладу процентов с учётом срока вклада с определённой договором банковского вклада периодичностью.
Чаще всего банки предлагают программы с ежемесячной капитализацией, при которой процентный доход рассчитывается по формуле:
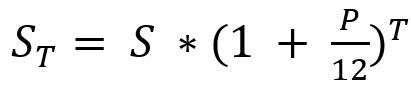
ST — итоговый доход, то есть размер вклада на конец срока, включая сумму открытия и начисленный процент;
S — начальный депозит;
P — годовая ставка, разделённая на 100 (выраженная десятичной дробью);
T — срок договора в месяцах.
Рассчитаем итоговую сумму с теми же исходными данными:
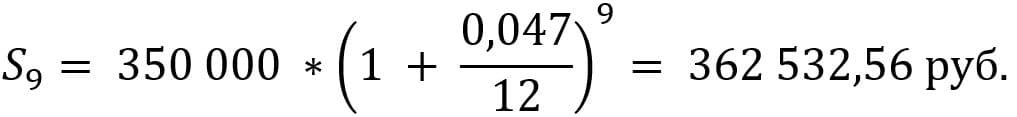
Процентный доход составит: 362 532,56 – 350 000 = 12 532,56 руб.
При начислении вознаграждения каждый квартал, а не раз в месяц, воспользуемся формулой:
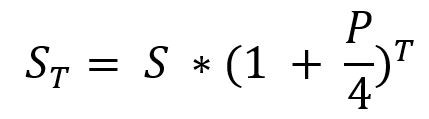
где Т — количество кварталов в сроке, остальные обозначения прежние.
Рассчитаем тот же вклад на конец срока.
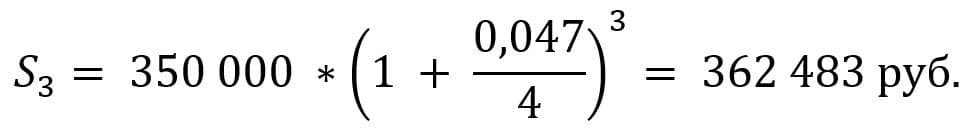
Доход в виде процентов в данном случае составит 12 483 руб.
В этом примере выгоднее оказался депозит со сложной процентной ставкой при условии ежемесячной капитализации.
Пример 2. Иван Иванович (И.И.) за внедрение рационализаторского предложения получил премию в размере 200 000 руб. Увидел по телевизору рекламу банка Х о супервыгодных условиях вклада под 6% годовых с условием размещения депозита на три года.
Рассчитаем доход И.И. от данного предложения при условии простых процентов.
Ежегодный доход составит: 200 000 * 6 / 100 = 12 000 руб.
Доход за три года: 36 000 руб.
К концу третьего года на счёте И.И.: 200 000 + 36 000 = 236 000 руб.
Таким образом, для расчёта суммы вклада через n лет под P% можно воспользоваться формулой:
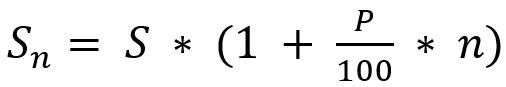
Выполним расчёт дохода И.И. при условии использования сложных процентов с капитализацией в конце года.
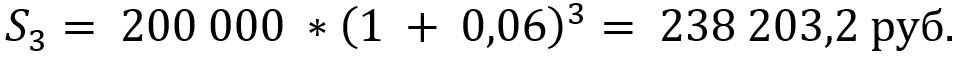
Доход на конец срока в данном случае составит 38 203,2 руб.
Интересно увидеть доход с ежемесячной капитализацией, вот расчёт:
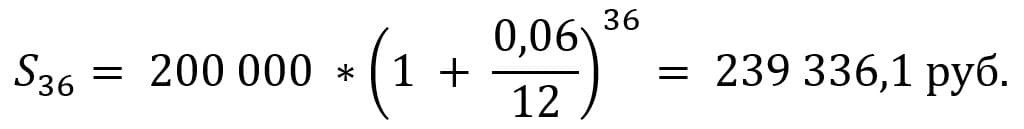
Доход за три года составит 39 336,1 руб.
На что обратить внимание
Мы на примерах показали различие между простой и сложной процентными ставками. Представленные расчёты убеждают в эффективности сложной процентной ставки.
Следует учесть: чем дольше срок размещения депозита, тем выше ставка. Поэтому необходимо сравнивать условия с фактической ставкой, применяемой по выбранным условиям в выбранном банке, и анализировать предложения по вкладам, обращая внимание на все условия, касающиеся будущей доходности.
Функция Excel – это специальная
формула, хранящаяся в памяти
приложения Excel. Каждая функция
включает две части:
• имя функции (например, СУММ);
• аргументы.
Имя описывает операцию, которую
эта функция выполняет. Аргументы
– это данные, которые используются
функцией для получения результата.
2
3. 2. Мастер функций
Для запуска Мастера функций, можно
воспользоваться одним из следующих
способов:
• щелкнуть мышью по кнопке Мастер
функций на панели инструментов
Excel. На ней изображены символы fx ;
• выполнить команду Вставка –
Функция.
3
4. Работа Мастера функций состоит из двух шагов. Сразу же после его запуска открывается первое диалоговое окно вида:
5. Второе окно Мастера функций содержит поля для ввода аргументов выбранной функции.
6. ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ФУНКЦИЙ EXCEL
7. Пример1. Использование функции ЕСЛИ
ЗАДАНИЕ.
Для следующей ниже таблицы
вычислить величину скидки, которая
определяется по правилу: если
заказчик заплатил сумму,
превышающую 1000$, скидка составит
20%, в противном случае – 10%.
7
9. Пример 2. Использование функций работы с датами
11. Финансовые функции Excel
• В пакете Microsoft Excel для выполнения
финансовых расчетов имеется специальная
группа функций, получивших название
финансовых.
• С помощью финансовых функций
осуществляются такие типичные финансовые
расчеты, как: вычисление суммы платежа
по погашению ссуды (кредита), стоимость
вложения или ссуды по прошествии
некоторого времени и др.
11
12. Для вычисления характеристик финансовых операций удобно использовать функции Б3, КПЕР, HOPMA, П3, ПЛТ
Наименование
функции
БЗ (будущая
стоимость)
КПЕР (количество
периодов)
НОРМА (процентная
ставка)
ПЗ (сегодняшняя
стоимость)
ПЛТ (размер платежа)
Формат функции
Б3 (БС)(ставка; кпер; платеж; нс; [тип])
КПЕР(ставка; платеж; нз; бс; [тип])
НОРМА (СТАВКА)(кпер; платеж; нз; бс;
[тип])
П3 (ПС)(ставка; кпер; платеж; бс; [тип])
ПЛТ (ППЛАТ)(ставка; кпер; нз; [бс];
[тип])
12
• Как следует из таблицы, большинство
функций имеют одинаковый набор базовых
аргументов:
• ставка - процентная ставка (норма
доходности заемных средств - i);
• кпер - срок (число периодов - n) проведения
операции;
• выплата - величина периодического
платежа;
• нз (нс) - начальное значение (величина PV);
• бз (бс) - будущее значение (FV);
• [тип] - тип начисления процентов (1 - начало
периода, 0 - конец периода), необязательный
аргумент.
13
14. Задание для самостоятельной работы
• Найти информацию о финансовых
функциях Excel и составить их описание;
• привести примеры использования
финансовых функций.
• Отчет должен быть представлен
преподавателю на бумажном носителе.
• При этом в текущем контроле оценивается
оригинальность выполнения задания,
интересные примеры, оригинальность
использованных литературных источников.
14
15. Пример 3. Использование функции БЗ
• Определить будущую величину вклада
в 10000 $, помещенного в банк на 5 лет
под 5% годовых, если начисление
процентов осуществляется:
а) раз в год;
б) раз в месяц.
15
17. Следует обратить особое внимание на способы задания аргументов.
• Значение процентной ставки (аргумент
ставка) обычно задается в виде
десятичной дроби:
• 5% - 0,05.
• Если начисление процентов
осуществляется m раз в год, аргументы
необходимо откорректировать
соответствующим образом:
• i = i/m;
• n = n m.
17
• Аргумент «начальное значение - нз»
здесь задан в виде отрицательной
величины (-10000), так как с точки
зрения вкладчика эта операция влечет
за собой отток его денежных средств в
текущем периоде с целью получения
положительной величины (12762,82)
через 5 лет.
18
• Однако для банка, определяющего будущую
сумму возврата средств по данному депозиту,
этот аргумент должен быть задан в виде
положительной величины, так как означает
поступление средств (увеличение пассивов):
• =БЗ(0,05; 5; 0; 10000) (Результат: -12762,82).
• Полученный же при этом результат отрицательная величина, так как операция
означает расходование средств (возврат денег
банком вкладчику).
19
20. Пример 4. Использование функции КПЕР
• По вкладу в 10000$, помещенному в
банк под 5% годовых, начисляемых
ежегодно, была выплачена сумма
12762,82$.
• Определить срок проведения операции.
20
22. Пример 5. Использование функции ППЛАТ (ПЛТ)
ЗАДАНИЕ.
Предположим, что магазин собирается
закупить 100 штук видеомагнитофонов по
цене 350$ за штуку. Он берет кредит в
350*100=35000$ под 12% годовых на срок
2 года. Каковы будут ежемесячные
выплаты магазина при погашении этого
кредита? Каковы будут ежемесячные
выплаты магазина при покупке другого
количества видеомагнитофонов?
22
23. Порядок выполнения действий.
• Ввести в ячейку F6 формулу: =F4*F5.
• Ввести в ячейку C4 формулу: =F6.
• Ввести в ячейку C8 формулу:
=ППЛАТ(C5/12; C6; C4). Появится число
–1647,57.
• Изменить в ячейке F5 число 100 на 80.
• Посмотреть, каковы будут новые
выплаты.
24
25. Пример 6. Финансовая задача
В сберегательном банке имеются два вида
денежных вкладов: простой и сложный
(иногда называется капитализированным).
Простой вклад составляет P1, сложный Р2 процентов в месяц. При простом
вкладе проценты начисляются от
первоначально вложенной суммы S0. При
сложном вкладе очередное начисление
осуществляется по итогам предыдущего,
т.е. происходит начисление процентов на
проценты.
25
Исследуйте финансовую модель для
ответа на вопрос:
Каким вкладом и в какие сроки выгодно
пользоваться?
Проведите исследования для
S0=1 000 000 руб; Р1=6%; Р2=4%.
26
27. Математическая модель
Простой вклад
Сложный вклад
А0=S0
В0=S0
А1=А0+А0*Р1/100
B1=B0(1+P2/100)
А2=А1+А0*Р1/100
B2=B1(1+P2/100)
…
…
АN=AN-1+A0*P1/100
BN=BN-1(1+P2/100)
27
• Соотношение простого и сложного
вкладов через N месяцев
определяется знаком разности
АN - BN.
• Математическая постановка
задачи: Определить значение N, при
котором изменяется знак разности
АN - BN .
28
29. Итак, необходимо заполнить таблицу следующего вида:
30. Пример 7. Расчет подоходного налога
Ставки подоходного налога
до 52 800 руб.
9%
от 52801 до 132000 руб.
4752+15% с суммы,
превышающей 52800
от 132001 до 184800 руб.
от 184801 до 237600 руб.
237 601 руб. и выше
16632+20% с суммы,
превышающей 132000
27192+25% с суммы,
превышающей 184800
40392+30% с суммы,
превышающей 237600
30
31. Формула для расчета подоходного налога:
32. Пример 8. Статистическая обработка результатов эксперимента
Методами статистической
обработки результатов
эксперимента называются
математические приемы, формулы,
способы количественных расчетов, с
помощью которых показатели,
получаемые в ходе эксперимента,
можно обобщать, приводить в систему,
выявляя скрытые в них
закономерности.
32
33. Выборочное среднее значение
• Выборочное среднее значение как
статистический показатель представляет собой
среднюю оценку.
• Эта оценка может характеризовать, например,
степень развития некоторого качества в целом у
той группы людей, которая была подвергнута
психодиагностическому обследованию.
• Сравнивая непосредственно средние значения
двух или нескольких выборок, можно судить об
относительной степени развития у людей,
составляющих эти выборки, оцениваемого
качества.
33
34. Выборочное среднее определяется при помощи следующей формулы:
n
Xср=
1
xk
n k 1
где
Хср – выборочная средняя величина по
выборке;
n – количество элементов в выборке;
хk – частные значения элементов
выборки.
34
35. Пример.
Допустим, что в результате применения
психодиагностической методики для
оценки некоторого психологического
свойства у десяти испытуемых мы
получили следующие показатели
степени развитости данного свойства:
х1=5, x2=4, x3=5, х4=6, x5=7, x6=3, х7=6,
x8=2, x9=8, x10=4
Получим: Хср=5,0.
35
36. Дисперсия
Дисперсия как статистическая величина
характеризует, насколько частные значения
отклоняются от средней величины в данной
выборке. Чем больше дисперсия, тем больше
отклонения или разброс.
Дисперсия вычисляется по следующей формуле:
n
1
2
2
S ( x k X ср )
n k 1
36
37. Пример.
Пусть х1=5, x2=4, x3=5, х4=6, x5=7, x6=3, х7=6,
x8=2, x9=8, x10=4
Мы видим, что все величины разные и
отличаются не только друг от друга, но и от
средней величины.
Меру их общего отличия от средней
величины и характеризует дисперсия. Ее
определяют для того, чтобы можно было
отличать друг от друга величины, имеющие
одинаковую среднюю, но разный разброс.
37
Представим себе другую, отличную от
предыдущей, выборку первичных
значений, например, такую:
х1=5, x2=4, x3=5, х4=6, x5=5, x6=6, х7=5, x8=4,
x9=5, x10=5
Легко убедиться в том, что ее средняя
величина также равна 5,0. Но в данной
выборке ее отдельные частные значения
отличаются от средней гораздо меньше,
чем в первой выборке.
38
Задача 1.Вы поместили в банк вклад 100 тыс. руб. под простую процентную ставку 6% годовых. Какая сумма будет на счете через 3 года? Какова величина начисленных процентов?
Решение
По формуле (1.1.) при Р=100 тыс. руб., n=3, r =0,06 получаем :
F=100 ×(1+3×0,06)=118 тыс. руб.
Через три года на счете накопится 118 тыс. рублей.
Величина начисленных за три года процентов составит:
118 -100=18 тыс. руб.
Задача 2.На какой срок необходимо поместить денежную сумму под простую процентную ставку 8% годовых, чтобы она увеличилась в 2 раза?
Решение
Искомый срок определяем из равенства множителя наращения величине 2 :
1+n×0,08=2, поэтому
n=1/0,08=12,5 лет.
Сумма, размещенная в банке под 8% годовых, в два раза увеличится через 12,5 лет.
Задача 3.Ссуда в сумме 3000 долл. предоставлена 16 января с погашением через 9 месяцев под 25 % годовых (год не високосный). Рассчитайте сумму к погашению при различных способах начисления процентов : а) обыкновенный процент с точным числом дней; б) обыкновенный процент с приближенным числом дней; в) точный процент с точным числом дней .
а) По формуле (1.3), используя обыкновенный процент с точным числом дней, рассчитанным по финансовым таблицам (t=289-16=273 дня), получим:
F=3000∙(1+0,25×273/360=3568,75 долл.
Сумма к погашению равна 3568,75 долл.
б) По формуле (1.3), используя обыкновенный процент с приближенным числом дней, рассчитанным по финансовым таблицам (t=9×30=270 дня),получим:
F=3000∙ (1+0,25×270/360)=3562,5 долл.
Сумма к погашению равна 3562,5 долл.
в) По формуле (1.3), используя точный процент с точным числом дней, рассчитанным по финансовым таблицам (t=289-16=273 дня), получим:
F=3000∙ (1+0,25×273/365)=3560,96 долл.
Сумма к погашению равна 3560,96 долл.
Задача 4.В финансовом договоре клиента с банком предусмотрено погашение долга в размере 8,9 тыс. руб. через 120 дней при взятом кредите в размере 8 тыс. руб. Определить доходность такой сделки для банка в виде годовой процентной ставки при использовании банком простых обыкновенных процентов.
Решение
По формуле (1.5) при F=8,9 тыс. руб., P= 8 тыс. руб., t= 120 дней, T=360 дней, получим :
r=360×(8,9-8)/ (8×120)= 0,3375=33,75%.
Доходность банка составит 33,75 процентов годовых.
Задача 5.Господин Х поместил 160 тыс. руб. в банк на следующих условиях: в первые полгода процентная ставка равна 8% годовых, каждый следующий квартал ставка повышается на 1%. Какая сумма будет на счете через полтора года, если проценты начисляются на первоначальную сумму вклада? Какую постоянную ставку должен использовать банк, чтобы сумма по вкладу не изменилась?
Решение
Применяя формулу (1.4), получим :
F=160×(1+0,5×0,08+0,25×0,09×+0,25×0,1+0,25×0,11+0,25×0,12)= 183,2
Через полтора года на счете накопится 183 200 руб.
Постоянную ставку, которую должен использовать банк, для того чтобы сумма, накопленная на счете, не изменилась, находим из уравнения:
r=0,096667=,9,67%
Постоянная ставка, которую должен использовать банк, для того чтобы сумма, накопленная на счете, не изменилась, равна 9,67 % годовых.
Задача 6.Кредит выдается под простую ссудную ставку 24 % годовых на 250 дней. Рассчитать сумму, полученную заемщиком, и сумму процентных денег, если необходимо возвратить 3500 тыс. руб.
Задача 1.На депозит поместили 300 тыс. руб. на полтора года. Банк начисляет простые учетные проценты по ставке под 14% годовых. Определить наращенную сумму с учетом уплаты налога на проценты, если ставка налога на проценты составляет 12% годовых.
Решение
Используем формулу (8.4)при P=300; n=1,5; t=0,12; d=0,14
Наращенная сумма с учетом налога на проценты составит 370018 руб.
Задача 2.На депозит поместили 300 тыс. руб. на полтора года. Банк начисляет простые проценты по ставке под 16% годовых. Определить наращенную сумму с учетом уплаты налога на проценты, если ставка налога на проценты составляет 12% годовых.
Решение
Используем формулу (8.2) при P=300; n=1,5; t=0,12; r=0,16
Наращенная сумма с учетом налога на проценты составит 360336 руб.
Задача 3.На вклад в 2 млн. руб. в течение 4 лет каждые полгода начислялись сложные проценты по годовой номинальной ставке 12% годовых. Определить наращенную сумму после уплаты налога на проценты, если ставка налога на проценты составляет 8% годовых.
Решение
Запишемформулу (8.6) с учетом полугодового начисления процентов:
при P=2; r=0,12; n=4; m=2; t=0,08
Наращенная сумма с учетом налога на проценты составит 3 092 680руб.
Задача 4.Для участия в некотором проекте предпринимателю необходимо 280 тыс. руб. Между тем он располагает суммой 250 тыс. руб. С целью накопления необходимой суммы предприниматель собирается положить 250 тыс. руб. в банк. Предлагаемая банком ставка по вкладам равна 14% годовых. Какое количество дней необходимо для накопления требуемой суммы с учетом уплаты налога на проценты, если банк начисляет простые проценты, использует точный процент с точным числом дней, а ставка налога на проценты равна 1%?
Решение
Обозначим через Х необходимое число дней, тогда формула (8.2) запишется в виде:
При Ft =280; Р=250; r=0,14; t=0,01
280=250∙[1+0,014∙(1-0,01)X / 365]
Решая полученное уравнение относительно Х, получаем:
Для накопления требуемой суммы необходимо 317 дней.
Задача 5.Клиент положил в банк 60 тыс. рублей под простую процентную ставку 10% годовых и через полгода с учетом налога на проценты получил 62,8 тыс. руб. Определить ставку налога на проценты.
Б) Присвоить листу имя Торговля и производство.
В) Просуммировать данные по показателям «Торговля» и «Производство».
Г). Вычислить «Долю торговли».
Указание. При вычислении «Доли торговли» содержимое столбца «Торговля» делится на содержимое столбца «Производство».
Д). Отформатировать таблицу, применив к столбцам «Торговля» и «Производство» денежный формат, а к столбцу «Доля торговли» – процентный.
Таблица должна иметь следующий вид:
| Год | Торговля | Производство | Доля торговли |
| 66 174 тыс. руб. | 1 230 000 тыс.руб. | 5,38 % | |
| Всего | 1 828 990 тыс. руб. | 14 480 000 тыс. руб. | 12,63 % |
Сохранить таблицу в своей папке в файле с именем Лабораторная работа № 2.
Задание 5. На новом листе с именем Север составить таблицу сведений о прибыли от продаж видеофильмов фирмы «Север» в следующем виде:
| 6 янв 98 | 7 янв 98 | 8 янв 98 | 9 янв 98 | 10 янв 98 | 11 янв 98 | 12 янв 98 | |
| Драма | 122,56 | 178,05 | 165,4 | 11,58 | 210,48 | 255,88 | 88,25 |
| Комедия | 87,25 | 100,56 | 180,47 | 245,37 | 305,57 | 370,18 | 222,78 |
| Научная фантастика | 36,88 | 66,66 | 88,33 | 117,89 | 118,25 | 200,39 | 123,78 |
| Боевик | 110,37 | 285,47 | 177,89 | 305,27 | 279,27 | 279,80 | 355,87 |
| Другие | 66,44 | 71,29 | 117,84 | 188,77 | 360,01 | 410,54 | 265,67 |
| Итого | |||||||
| Налог | |||||||
| Всего |
Замечание. При вычислении Налога использовать абсолютный адрес для ссылки на ячейку, куда введена ставка налога (12%).
Результат сохранить в своей папке в файле с именем Лабораторная работа № 2.
Задание 6. На листе с именем Автомобили создать таблицу и отформатировать ее:
| Марка | 4-й квартал 2008 | 4-й квартал 2009 | Среднее значение |
| Объем | Доля | Объем | Доля |
| БМВ | |||
| Форд | |||
| Мерседес | |||
| Пежо | |||
| Рено | |||
| Ауди | |||
| Опель | |||
| Феррари | |||
| Всего: |
− ввести формулы для вычисления сумм по столбцам 2 и 4;
− вычислить «Долю» как отношение соответствующего объема продаж к значению «Всего»;
− вычислить «Среднее значение» как среднее между объемами продаж.
Результат сохранить в своей папке в файле с именем Лабораторная работа № 2.
Задание 7. На листе Книги заполнить и отформатировать следующую таблицу:
Список книг, купленных в январе
| № п/п | Название | Цена за единицу | Количество | Стоимость, долл. | Стоимость, бел. руб. |
| Маринина А. «Чужая маска» | 8,3 | ||||
| Бенцони Ж.«Марианна» | 7,2 | ||||
| Кинг Ст. «Ночная смена» | 14,2 | ||||
| Шелдон С. «Расколотые сны» | 10,0 | ||||
| Шелдон С.«Интриганка» | 12,0 | ||||
| Леонов Н. «Бросок кобры» | 8,9 | ||||
| Леонов Н. «Стервятники» | 8,4 | ||||
| Словин Л. «Расстояние в один вечер» | 6,3 | ||||
| Чейз Дж. Х. «Мертвые молчат» | 9,2 | ||||
| Незнанский Ф. «Последний маршал» | 7,1 |
а) вычислить «Стоимость в долларах»;
б) вычислить «Стоимость в бел. руб.» следующими способами:
− ввести в некоторую ободную ячейку вне таблицы значение «Курса доллара» и использовать адрес этой ячейки в расчетах;
− присвоить ячейке, содержащей «Курс доллара», имя и использовать его в расчетах.
Результат сохранить в своей папке в файле с именем Лабораторная работа № 2.
Задание 8. Финансовая задача
Постановка задачи: В сберегательном банке имеются два вида денежных вкладов: простой и сложный (иногда называется капитализированным). Простой вклад составляет P1, сложный – Р2 процентов в месяц. При простом вкладе проценты начисляются от первоначально вложенной суммы S0. При сложном вкладе очередное начисление осуществляется по итогам предыдущего, т. е. происходит начисление процентов на проценты.
Исследуйте финансовую модель для ответа на вопросы:
1. Каким вкладом и в какие сроки выгодно пользоваться?
2. Каков будет ответ на предыдущий вопрос, если начиная с K-го месяца, простой процент увеличился до S1, а сложный упал до S2?
3. Когда при таких изменениях сумма сложного вклада достигнет M рублей?
4. Когда сумма сложного вклада увеличится в 1,5 раза?
5. Проведите исследования для S0=1 000 000 руб; Р1=6; Р2=4; S1=6,5; S2=3,5;
K=4; М=2 000 000.
Математическая модель
Для поиска зависимости между исходными и конечными данными построим цепочку равенств:
| Простой вклад | Сложный вклад |
| А0=S0 | В0=S0 |
| А1=А0+А0*Р1/100 | B1=B0(1+P2/100) |
| А2=А1+А0*Р1/100 | B3=B1(1+P2/100) |
| … | … |
| АN=AN–1+A0*P1/100 | BN=BN-1(1+P2/100) |
| АN= S0*(1+N*P1/100) | BN= S0* (1+P2/100) N |
Соотношение простого и сложного вкладов через N месяцев определяется знаком разности АN – BN.
Математическая постановка задачи:
Определить значение N, при котором изменяется знак разности АN – BN .
Задание 9. Экологическая задача
Постановка задачи: В результате сброса промышленных стоков возрос уровень загрязнения реки. Каким он будет через сутки, двое, трое и т. д. и через сколько суток уровень загрязнения воды станет допустимым, если известно, что за сутки он уменьшается в К раз, начальная концентрация вредных примесей С0, предельно допустимая концентрация примесей – Сдоп.
Провести исследование экологической модели при следующих значениях параметров:
| Вещество | C0(мг/л) | Cдоп(мг/л) | K |
| Свинец | 0,03 | 1,12 | |
| Мышьяк | 1,5 | 0,05 | 1,05 |
| Фтор | 0,2 | 0,05 | 1,01 |
Задание 10. Задача «Преступность и судимость»
Отформатировать таблицу. Результат сохранить в своей папке в файле с именем Лабораторная работа № 2.
Лабораторная работа № 3
ФУНКЦИИ И СЛОЖНЫЕ ВЫчиСЛЕНИЯ В EXCEL (ЧАСТЬ 1)
Задания
Задание 1. На листе «Функции» выполнить следующие задания:
1. Вычислить в ячейках строки 1:
Sin 37 o , Cos 25 o , tg 132 o .
2. Вычислить в ячейках строки 2:
Ln 5,25; Log2372,3; e 7,05 .
3. Составить таблицу значений чисел:
7,2293; 18,992971; 15,32143,
округленных обычным способом, с недостатком и с избытком. Сохранить при этом 3 знака после запятой (использовать функции Округлвверх, Округлвниз).
4. Вывести в свободную ячейку сегодняшнюю дату.
5. Определить, каким днем недели было (функция Деньнед):
2 февраля 1907 года; 14 декабря 1938 года;
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
© cyberpedia.su 2017-2020 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!
Автор статьи

Читайте также:

