15 января планируется взять кредит в банке на 6 месяцев 1 млн рублей условия возврата
Обновлено: 26.07.2024
Встречаются задачи, в которых долг по кредиту уменьшается неравномерно, а убывает согласно данным, представленным в таблице.
Задачи для разбора взяты с сайта РЕШУ ЕГЭ .
Задача 1. Рассчитываем разницу между общей суммой выплат и суммой самого кредита
15 января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в процентах от кредита) | 100% | 90% | 80% | 70% | 60% | 50% | 0% |
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
При решении данной задачи воспользуемся советами, данными в прошлой статье «Проценты по кредиту с равными платежами».
Учитываем, что общая сумма выплат будет превышать сумму кредита за счёт начисленных и уплаченных процентов.
I способ — решим задачу в общем виде, приняв за сумму кредита S руб. р = 5% = 0,05,
Представим решение в виде таблицы.
| Долг с начисленными процентами, руб. | Выплата, руб. | Остаток долга, руб. | Остаток долга, % | |
| Февраль | Sr | Sr — 0,9S | 0,9S | 90% |
| Март | 0,9Sr | 0,9Sr — 0,8S | 0,8S | 80% |
| Апрель | 0,8Sr | 0,8Sr — 0,7S | 0,7S | 70% |
| Май | 0,7Sr | 0,7Sr — 0,6S | 0,6S | 60% |
| Июнь | 0,6Sr | 0,6S r — 0,5S | 0,5S | 50% |
| Июль | 0,5Sr | 0,5Sr | 0 | 0% |
Общая сумма выплат составит:

Общая сумма выплат от суммы кредита:

Следовательно, переплата равна 22,5%.
II способ — используем частный случай.
Пусть сумма кредита равна 100 руб.
| Долг с начисленными процентами, руб. | Выплата, руб. | Остаток долга, руб. | Остаток долга, % | |
| Февраль | 100 * 1,05 = 105 | 105 — 90 = 15 | 90 | 90% |
| Март | 90 * 1,05 = 94,5 | 94,5 — 80 = 14,5 | 80 | 80% |
| Апрель | 80 * 1,05 = 84 | 84 — 70 = 14 | 70 | 70% |
| Май | 70 * 1,05 = 73,5 | 73,5 — 60 = 13,5 | 60 | 60% |
| Июнь | 60 * 1,05 = 66,3 | 66,3 — 50 = 13 | 50 | 50% |
| Июль | 50 * 1,05 = 52,5 | 52,5 | 0 | 0% |
Общая сумма выплат:

Следовательно, переплата равна 22,5%.
Задача 2. Рассчитываем наибольшее значение процентов, при котором общая сумма выплат будет меньше заданного числа
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн руб. Условия его возврата таковы:
-
1—го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн руб.
Выплата, млн руб.
Остаток долга, млн руб.
Обратите внимание! Ежемесячная выплата рассчитывается как разность между долгом на начало месяца и остатком долга. Следовательно, третий столбец заполняется в последнюю очередь.
Общая суммы выплат:


Обратите внимание! Вычисление следует производить до тысячных.
По условию задачи, r — целое число, следовательно, r = 7%.
Еженедельная рассылка с лучшими материалами «Открытого журнала»
Без минимальной суммы, платы за обслуживание и скрытых комиссий
Для оформления продукта необходим брокерский счёт
проект «Открытие Инвестиции»
Открыть брокерский счёт
Тренировка на учебном счёте
Об «Открытие Инвестиции»
Москва, ул. Летниковская,
д. 2, стр. 4
8 800 500 99 66
Согласие на обработку персональных данных
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,25 млн рублей.
Решение:
r – процент банка по кредиту;
– число, на которое умножается долг, что бы получить проценты в рублях;
Составим таблицу, из которой найдём платёж каждого месяца:

Сложим все платежи :
По условию сумма выплат должна быть < 1,25млн. рублей:
умножим обе части неравенства на 1000
26r < 250
Ближайшее целое число в этом промежутке – 9. r = 9%.
15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что в течение первого года кредитования нужно вернуть банку 2466 тыс. рублей. Какую сумму нужно выплатить банку за последние 12 месяцев?
Источник: Ященко 2020 (10 вар), Ященко 2020 (14 вар), Ященко 2020 (36 вар), Ященко 2020 (50 вар), Ященко 2019 (14 вар), Ященко 2019 (50 вар), Ященко 2018 (20 вар), Ященко 2018 (30 вар), Ященко 2018 ( 36 вар).
Решение:
Обозначим:
S тыс. рублей – сумма кредита в банке на 24 месяца;
2% = 0,02 – процент на который возрастает долг каждый месяц.
Разберёмся сколько мы будем выплачивать каждый месяц.
«15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.»
Это означает, что каждый месяц мы должны выплачивать часть начального долга (S поделить на количество месяцев, т.е ) + начисленные % за этот месяц (0,02·долг). Задача на дифференцированный платёж.
Составим таблицу для первого года кредитования:
Сложим все платежи за первый год:
Сложив все получим ровно . А у % вынесем общий множитель по условию это равно 2466 тыс. рублей:
тыс. рублей
Составим аналогично сумму платежей за последние 12 месяцев и зная S, найдём какую сумму необходимо было выплатить:
Один из типов экономических задач — это задачи на платежи с равномерно убывающим долгом. Каждый месяц (период) основной долг уменьшается на одинаковую сумму. Ежемесячный платёж будет состоять из суммы основного долга и суммы начисленных процентов на остаток долга.
В этом случае мы имеем дело с дифференцированными платежами.
Внимание: в задачах этого типа применяется формула суммы n-первых членов арифметической прогрессии.
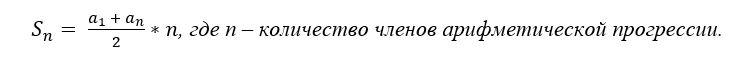
Задачи для разбора берутся из вариантов ЕГЭ прошлых лет, размещённых на популярном среди школьников и учителей сайте РЕШУ ЕГЭ .
Задача 1. Рассчитать сумму кредита
15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:
-
1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
Какую сумму следует взять в кредит, чтобы общая сумма выплат по кредиту после полного его погашения составила 2 млн руб. (никакие округления при вычислении платежей не производятся)?
S тыс. руб. — сумма кредита,
2 млн руб. = 2000 тыс. руб.,
X тыс. руб. — ежемесячная выплата основного долга.
Суммы ежемесячного долга: S; (S — X); (S — 2 * X . S — 47 * X); (S — 48 * X); 0
S * p; (S — X) * p; (S — 2 * X) * p . (S — 47 * X) * p; (S — 48 * X) * p; 0
Сумма выплат = Сумма кредита + Проценты

S * (1 + 49 * p — 24 * p) = 2000
S * (1 + 25 * 0,01) = 2000
S = 1600 тыс. руб., или 1,6 млн руб.
Ответ: 1,6 млн руб.
Задача 2. Рассчитать сумму кредита
15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
-
1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1,604 млн руб. (1604 тыс. руб.)?
Задача отличается от предыдущей — выплаты по основному долгу (30 тыс. руб.) осуществляются только первые 20 месяцев, а значит, в последний месяц выплата будет иной.
S тыс. руб. — сумма кредита
Суммы ежемесячного долга: S; (S — 30); (S — 60. S — 570); (S — 600); 0
Начисленные проценты: S * р; (S — 30) * р; (S — 60) * р. (S — 570) * р; (S — 600) * р; 0
Сумма выплат = Сумма кредита + Проценты


S * (1 + 21 * 0,03) — 0,03 * 6300 = 1604
1,63 * S — 189 = 1604
1,63 * S = 1604 + 189
S = 1100 тыс. руб., или 1,1 млн руб.
Ответ: 1,1 млн руб.
Задача 3. Рассчитать, на сколько месяцев планируется взять кредит
15 января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условия его выплаты таковы:
-
1-го числа n-ого месяца долг возрастёт на 3% по сравнению с концом предыдущего месяца;
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?

Превышение выплат на 30% от суммы кредита — за счёт выплаченных процентов.
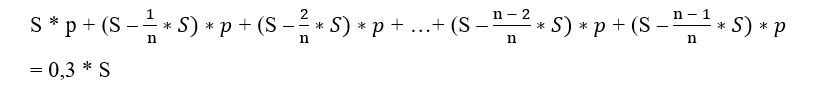
Раскрываем скобки и группируем слагаемые.

Ответ: 19 месяцев.
Еженедельная рассылка с лучшими материалами «Открытого журнала»
Без минимальной суммы, платы за обслуживание и скрытых комиссий
Для оформления продукта необходим брокерский счёт
проект «Открытие Инвестиции»
Открыть брокерский счёт
Тренировка на учебном счёте
Об «Открытие Инвестиции»
Москва, ул. Летниковская,
д. 2, стр. 4
8 800 500 99 66
Согласие на обработку персональных данных
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Стихи и цветы,поздравления и сценарии. Школьная математика, подготовка к ЕГЭ и ГИА,тесты, проекты,задачи и решения. Собственные произведения и фотографии моих цветов: георгины и розы.
суббота, 14 апреля 2018 г.
Примеры оценивания решений задания 17
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.


Модель построена неверно. Если подставить вместо r число 3 в таблицу, то сумма долга уже на 1 число второго месяца должна составить 4 млн рублей, кроме того, еще и неравенство решено неверно.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.

Модель построена верно. Усложняет проверку отсутствие вычислений. В таблице все результаты вычислений по формулам, записанным справа, верные. Логика решения верна.
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.
Автор статьи

Читайте также:

