В июле планируется взять кредит в банке на 13 лет условия его возврата таковы
Обновлено: 26.07.2024

Задание 15 № 526256
В июле планируется взять кредит в банке на срок 15 лет. Условия его возврата таковы:
— каждый январь долг возрастает на x% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найдите x, если известно, что за весь период выплатили на 15% больше, чем взяли в кредит.
Пусть начальная сумма кредита равна S0, тогда переплата за первый год равна По условию, ежегодный долг перед банком должен уменьшиться равномерно. Этот долг состоит из двух частей: постоянной ежегодной выплаты, равной S0/15, и ежегодной равномерно уменьшающейся выплаты процентов, равной
Используя формулу суммы членов арифметической прогрессии, найдём полную переплату по кредиту:
По условию общая сумма выплат на 15% больше суммы, взятой в кредит, тогда:
Примечание Дмитрия Гущина.
Укажем общие формулы для решения задач этого типа. Пусть на n платежных периодов (дней, месяцев, лет) в кредит взята сумма S, причём каждый платежный период долг сначала возрастёт на x% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же сумму меньше долга на конец предыдущего платежного периода. Тогда величина переплаты П и полная величина выплат В за всё время выплаты кредита даются формулами
В условиях нашей задачи получаем: откуда для n = 15 находим x = 1,875.
Доказательство формул (для получения полного балла его нужно приводить на экзамене) немедленно следует из вышеприведённого решения задачи путём замены 15 лет на n лет и использовании формулы суммы n первых членов арифметической прогрессии.

Задание 15 № 526256
В июле планируется взять кредит в банке на срок 15 лет. Условия его возврата таковы:
— каждый январь долг возрастает на x% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найдите x, если известно, что за весь период выплатили на 15% больше, чем взяли в кредит.
Пусть начальная сумма кредита равна S0, тогда переплата за первый год равна По условию, ежегодный долг перед банком должен уменьшиться равномерно. Этот долг состоит из двух частей: постоянной ежегодной выплаты, равной S0/15, и ежегодной равномерно уменьшающейся выплаты процентов, равной
Используя формулу суммы членов арифметической прогрессии, найдём полную переплату по кредиту:
По условию общая сумма выплат на 15% больше суммы, взятой в кредит, тогда:
Примечание Дмитрия Гущина.
Укажем общие формулы для решения задач этого типа. Пусть на n платежных периодов (дней, месяцев, лет) в кредит взята сумма S, причём каждый платежный период долг сначала возрастёт на x% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же сумму меньше долга на конец предыдущего платежного периода. Тогда величина переплаты П и полная величина выплат В за всё время выплаты кредита даются формулами
В условиях нашей задачи получаем: откуда для n = 15 находим x = 1,875.
Доказательство формул (для получения полного балла его нужно приводить на экзамене) немедленно следует из вышеприведённого решения задачи путём замены 15 лет на n лет и использовании формулы суммы n первых членов арифметической прогрессии.

Задания Д16 C5 № 544277
В июле планируется взять кредит в банке на сумму 1,6 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 12,5% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж в 2 раза больше наименьшего?
Пусть кредит взят на n лет, сумма кредита равна S = 1,6 млн руб. Повышающий коэффициент равен
Составим таблицу по данным задачи.
года
(с учетом процентов),
млн руб.
млн руб.
(после платежа),
млн руб.
Наибольшим является первый платёж, наименьшим — последний, тогда
Суммируем все выплаты:
Подставим числовые значения:
Ответ: 2,7 млн руб.

Задание 15 № 517569
В июле планируется взять кредит в банке на сумму 18 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если общая сумма выплат после полного погашения кредита составила 27 млн рублей?
По формуле для переплаты П при выплате суммы кредита S = 18 млн рублей дифференцированными платежами имеем:
где n — искомое число лет, а r = 10 — величина платежной ставки в процентах (см. Гущин Д. Д. «Встречи с финансовой математикой»; для получения полного балла доказательство этих формул необходимо приводить на экзамене). По условию, переплата П равна млн рублей
откуда n = 9.
Приведем другое решение.
Долг уменьшается каждый июль равномерно:
В январе долг возрастает на 10%, значит, долг в январе:
Скажите пожалуйста, разве на экзамене можно пользоваться формулой переплаты в готовом виде?
С 2018 года «формулу Гущина» надо выводить, иначе один балл снимут за недостаточное обоснование.

Задание 15 № 526293
В июле планируется взять кредит в банке на сумму 3 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 0,24 млн рублей? (Считайте, что округления при вычислении платежей не производятся).
Пусть кредит взят на n лет. Тогда долг (в млн руб) уменьшается каждый июль равномерно:
В январе долг возрастает на 20%, значит, долг (в млн руб) в январе:
Выплаты (в млн руб):
Тогда сумма выплат (в млн руб) равна
Наименьшим годовым платежом является последний платёж, значит, откуда
Тогда сумма выплат за 15 лет равна: (млн руб).
Ответ: 7,8 млн руб.
По сути решения это задание аналогично заданию 517480 из ЕГЭ 2017 года.
Источник: Основная волна ЕГЭ по математике 29.05.2019. Санкт-Петербург, Основная волна ЕГЭ по математике 29.05.2019. Вариант 316, Задания 17 (С5) ЕГЭ 2019

Задание 15 № 526335
В июле планируется взять кредит в банке на сумму 8 млн рублей на срок 4 года. Условия его возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 4 млн рублей, а наименьший — не менее 2,5 млн рублей.
Пусть Тогда увеличение суммы на r% эквивалентно её умножению на p. Пусть сумма, взятая в кредит, равна S. Заполним следующую таблицу
| Период | Долг на начало периода | Долг после начисления процентов | Выплата |
|---|---|---|---|
| 1 | S | Sp | |
| 2 | |||
| 3 | |||
| 4 |
т. к. т. е. выплата следующего периода меньше выплаты предыдущего. Значит, наибольшая выплата — первая, а наименьшая — последняя.
Следовательно, Теперь найдём r.
Аналоги к заданию № 526219: 526335 Все

Задание 15 № 526532
В июле планируется взять кредит в банке на сумму 14 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 3,85 млн рублей? (Считайте, что округления при вычислении платежей не производятся).
Пусть кредит взят на n лет. Тогда долг (в млн руб) уменьшается каждый июль равномерно:
По условию, каждый январь долг возрастает на 10%, значит, последовательность размеров долга (в млн рублей) в январе такова:
Следовательно, выплаты (в млн руб) должны быть следующими:
Получаем: откуда Значит, всего следует выплатить
Ответ: 17,5 млн руб.
По сути решения это задание аналогично заданию 517480 из ЕГЭ 2017 года.

Задание 15 № 521918
В июле планируется взять кредит в банке на сумму 20 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 47 млн рублей?
По формуле для переплаты П при выплате суммы кредита S = 20 млн рублей дифференцированными платежами имеем:
где n — искомое число месяцев, а r = 30 — величина платежной ставки в процентах (см. Гущин Д. Д. «Встречи с финансовой математикой»; для получения полного балла доказательство этих формул необходимо приводить на экзамене). По условию, переплата П равна млн рублей
откуда n = 8.

Задания Д16 C5 № 527505
В июле планируется взять кредит в банке на сумму 12 млн рублей на 15 лет. Условия его возврата таковы:
— пока долг больше половины исходной суммы, каждый январь он возрастает на 12% по сравнению с концом предыдущего года;
— если долг меньше половины исходной суммы, то каждый январь он возрастает на 4% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого последующего года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Какую сумму нужно вернуть банку?
Обозначим Размер долга после выплаты должен будет составлять . 0. До долга размер долга будет больше половины исходной суммы, поэтому банк будет умножать размер долга на p. Значит, выплаты будут
После этого размер долга будет меньше половины суммы и умножать банк будет на q. Значит, выплаты будут
И первая и вторая последовательность выплат — арифметические прогрессии. Посчитаем тогда общую сумму выплат:
Ответ: 21728000 рублей.

Задание 15 № 517203
В июле планируется взять кредит в банке на сумму 7 млн рублей на срок 10 лет. Условия возврата таковы:
— каждый январь долг возрастает на r % по сравнению с концом предыдущего года;
— с февраля по июнь необходимо выплатить часть долга так, чтобы на начало июля каждого года долг уменьшался на одну и ту же сумму по сравнению с предыдущим июлем.
Найдите наименьшую возможную ставку r , если известно, что последний платёж будет не менее 0,819 млн рублей.
Долг перед банком (в млн рублей) по состоянию на июль должен уменьшаться до нуля равномерно:
7; 6,3; 5,6; . ; 1,4; 0,7; 0.
По условию каждый январь долг возрастает на r %. Пусть тогда последовательность размеров долга (в млн рублей) в январе такова:
7k; 6,3k; 5,6k; . ; 1,4k; 0,7k.
Следовательно, последний платеж составит 0,7k млн рублей.
Получаем откуда Значит,

Задание 15 № 517241
В июле планируется взять кредит в банке на сумму 8 млн рублей на срок 10 лет. Условия возврата таковы:
— каждый январь долг возрастает на r % по сравнению с концом предыдущего года;
— с февраля по июнь необходимо выплатить часть долга так, чтобы на начало июля каждого года долг уменьшался на одну и ту же сумму по сравнению с предыдущим июлем.
Найдите наименьшую возможную ставку r , если известно, что последний платёж будет не менее 0,92 млн рублей.
Долг перед банком (в млн рублей) по состоянию на июль должен уменьшаться до нуля равномерно:
8; 7,2; 6,4; . ; 1,6; 0,8; 0.
По условию каждый январь долг возрастает на r %. Пусть тогда последовательность размеров долга (в млн рублей) в январе такова:
8k; 7,2k; 6,4k; . ; 1,6k; 0,8k.
Следовательно, последний платеж составит 0,8k млн рублей.
Получаем откуда Значит,

Задание 15 № 526219
В июле планируется взять кредит в банке на сумму 6 млн рублей на срок 15 лет. Условия его возврата таковы:
— каждый январь долг возрастает на x% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найдите x, если известно, что наибольший платёж по кредиту составит не более 1,9 млн рублей, а наименьший — не менее 0,5 млн рублей.
Наибольший платеж за пользование кредитом будет выплачен в первый год, а наименьший — в последний. Долг перед банком по состоянию на июль должен уменьшаться до нуля равномерно, ежегодно уменьшаясь на одну пятнадцатую. Поэтому первый платеж составит одну пятнадцатую от 6 миллионов (возврат первой части тела долга) и процент за их использование: Последний платеж также составит одну пятнадцатую от 6 миллионов (возврат последней части тела долга) и процент за использование этой суммы в течение последнего года: Поскольку первая из найденных величин не больше 1,9 млн руб, а вторая не меньше 0,5 млн руб, получаем два линейных неравенства, откуда, соответственно, находим: и Тогда
Один из типов экономических задач — это задачи на платежи с равномерно убывающим долгом. Каждый месяц (период) основной долг уменьшается на одинаковую сумму. Ежемесячный платёж будет состоять из суммы основного долга и суммы начисленных процентов на остаток долга.
В этом случае мы имеем дело с дифференцированными платежами.
Внимание: в задачах этого типа применяется формула суммы n-первых членов арифметической прогрессии.
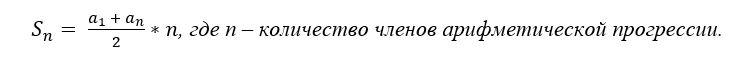
Задачи для разбора берутся из вариантов ЕГЭ прошлых лет, размещённых на популярном среди школьников и учителей сайте РЕШУ ЕГЭ .
Задача 1. Рассчитать сумму кредита
15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:
-
1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
Какую сумму следует взять в кредит, чтобы общая сумма выплат по кредиту после полного его погашения составила 2 млн руб. (никакие округления при вычислении платежей не производятся)?
S тыс. руб. — сумма кредита,
2 млн руб. = 2000 тыс. руб.,
X тыс. руб. — ежемесячная выплата основного долга.
Суммы ежемесячного долга: S; (S — X); (S — 2 * X . S — 47 * X); (S — 48 * X); 0
S * p; (S — X) * p; (S — 2 * X) * p . (S — 47 * X) * p; (S — 48 * X) * p; 0
Сумма выплат = Сумма кредита + Проценты

S * (1 + 49 * p — 24 * p) = 2000
S * (1 + 25 * 0,01) = 2000
S = 1600 тыс. руб., или 1,6 млн руб.
Ответ: 1,6 млн руб.
Задача 2. Рассчитать сумму кредита
15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
-
1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1,604 млн руб. (1604 тыс. руб.)?
Задача отличается от предыдущей — выплаты по основному долгу (30 тыс. руб.) осуществляются только первые 20 месяцев, а значит, в последний месяц выплата будет иной.
S тыс. руб. — сумма кредита
Суммы ежемесячного долга: S; (S — 30); (S — 60. S — 570); (S — 600); 0
Начисленные проценты: S * р; (S — 30) * р; (S — 60) * р. (S — 570) * р; (S — 600) * р; 0
Сумма выплат = Сумма кредита + Проценты


S * (1 + 21 * 0,03) — 0,03 * 6300 = 1604
1,63 * S — 189 = 1604
1,63 * S = 1604 + 189
S = 1100 тыс. руб., или 1,1 млн руб.
Ответ: 1,1 млн руб.
Задача 3. Рассчитать, на сколько месяцев планируется взять кредит
15 января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условия его выплаты таковы:
-
1-го числа n-ого месяца долг возрастёт на 3% по сравнению с концом предыдущего месяца;
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?

Превышение выплат на 30% от суммы кредита — за счёт выплаченных процентов.
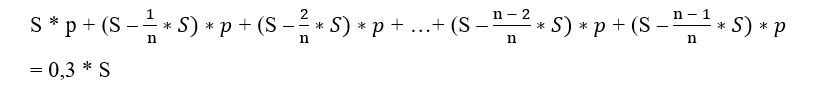
Раскрываем скобки и группируем слагаемые.

Ответ: 19 месяцев.
Еженедельная рассылка с лучшими материалами «Открытого журнала»
Без минимальной суммы, платы за обслуживание и скрытых комиссий
Для оформления продукта необходим брокерский счёт
проект «Открытие Инвестиции»
Открыть брокерский счёт
Тренировка на учебном счёте
Об «Открытие Инвестиции»
Москва, ул. Летниковская,
д. 2, стр. 4
8 800 500 99 66
Согласие на обработку персональных данных
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Каждый год долг увеличивается в 1+0.1=1.1 раз. По условию, долг уменьшается равномерно. Значит после первой выплаты сумма долга станет равна 3-(3/4)=2.25, после второй 3-2·(3/4)=1.5 и т.д.
Расписываем каждую выплату:
1) 3·1.1-x₁=2.25 ⇒ x₁=3.3-2.25=1.05 млн
2) 2.25·1.1-x₂=1.5 ⇒ x₂=2.475-1.5=0.975 млн
3) 1,5·1.1-x₃=0.75 ⇒ x₃=1.65-0.75=0.9 млн
4) 0.75·1.1-x₄=0 ⇒ x₄=0.825 млн
Сумма всех выплат составит
x₁+x₂+x₃+x₄=1.05+0.975+0.9+0.825=3.75 млн
Ответ: 3.75 млн р.


Кредит S= 3 млн.руб.
Тогда погашение кредита (без учета процентов) при условии уменьшения долга на одну и ту же величину будет выглятеть так
т.е. долг уменьшается равномерно на 1/4 часть
Теперь начислим на долг проценты
Тогда сумма всех выплат составит
И теперь 1.25*S=1.25*3=3.75 млн.руб.
Новые вопросы в Алгебра
Достатній рівень (3 бали)7. Знайдіть косинус кута мiж векторами й(-3; 0; 4) 1 5 (1; -2; 2). 8. Знайдіть значення m при яких вектори а(2:1; -2)1 Б (-4; … mi n) сколiнеарними.Високий рівень (3 бали) 9. Дано точки А(1; 0:0), В(0:0;1), C(0; 1:1), D(1:1:0). Знайдіть площу чотирикутника ABCD.
знайдіть похідну функцій:[tex]y = 8
Зі скриньки, у якій містяться 10 зелених та 8 блакитних кульок, навмання вийнято одну кульку. Яка ймовірність того, що ця кулька: 1) зелена; 2) блакит … на; 3) червона?
Скільки розв'язків має система двох лінійних рівнянь з двома змінними, якщо графіки рівнянь мають вигляд зображений на рис ДАЮ 20БАЛЛОВ 1 жодного 2 3
Автор статьи

Читайте также:

