В мае планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок
Обновлено: 26.07.2024
Приветствую! Меня зовут Александр Георгиевич. Я - репетитор по математике, информатике, программированию, алгоритмам и базам данных. Уже свыше 10 лет провожу подготовку школьников к рубежным экзамена ОГЭ/ЕГЭ по математике/информатике.
Для своих потенциальных клиентов я разработал многофакторную систему, которая позволит вам подобрать стоимость частных уроков, учитывая все ваши пожелания и ограничения.
Также настоятельно рекомендую вам потратить буквально пару минут собственного времени и познакомиться с отзывами школьников/студентов, занимающихся под моим началом. Все они достигли положительных результатов. Думаю, что у вас тоже получится!
На официальном экзамене ЕГЭ по математике в обязательном порядке придется столкнуться с задачей из экономического блока, поэтому, если у вас имеются какие-либо трудности с финансовыми задачами, то берите в руки мобильный телефон, набирайте мой контактный номер и записывайтесь на первый пробный урок.
Условие задачи
В июле планируется взять кредит в банке на сумму $6$ миллионов рублей на некоторый срок.
Условия его возврата таковы:
Каждый январь долг возрастает на $20\%$ по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил $1.8$ миллиона рублей?
Решение задачи
Во-первых, прочитав внимательно несколько раз условие задачи, нужно понять, к какому типу кредитования относится эта задача. Очевидно, что речь идет про кредит, который будет выплачиваться дифференцируемыми платежами. Главный маркер, на основании которого можно сделать такой вывод, заключен в этом предложении: "В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года".
Во-вторых, если вы достаточно плохо знаете схему дифференцированных платежей, часто путаетесь в ней, то в обязательном порядке познакомьтесь с моей информационной статьей, в которой детализировано изложен принцип работы дифференцированных платежей, а также построена математическая модель данной схемы. Обязательно прочтите и вы моментально станете сильнее в этой области!
Давайте введем следующие обозначения:
| \(S\) - размер первоначального кредита | \(r\) - процентная ставка банка, выраженная в долях | \(R = 1 + r\) - для удобства расчетов |
| \(n\) - общее количество отчетных периодов | \(i\) - номер текущего отчетного периода | \(\%_\) - размер начисленных банком процентов за конкретный период |
| \(p_\) - размер платежа за конкретный период | \(P\) - общая сумма всех выплат/платежей | \(q\) - ставка банка, выраженная в процентах |
Сразу хочу заметить, что не все обозначенные переменные нам пригодятся в процессе решении задачи, но точно большая часть из них.
Из условия вытекает, что:
| $S = 6$, млн. рублей | $q = 20\%$ | $r = \frac = \frac = 0.2$ | $i = 1$ |
Наша задача определить $n$, то есть количество отчетных периодов, и, что немаловажно, это значение должно быть минимальным!
На данный момент, пользуясь только этой информацией, решить задачу в принципе невозможно, но на помощь приходит важнейшее ограничение, а именно: "наибольший годовой платеж по кредиту не превысил $1.8$ миллиона рублей". Сейчас все встало на свои места.
Если вы хорошо понимаете модель дифференцируемых платежей, то помните о том, что в данной модели наибольшим платежом является самый $1$-ый платеж. Также, в качестве справочной информации, напомню, что наименьшим по размеру является последний платеж.
В ограничении говорится, что платеж не превысил некоторое значение, это задает нестрогое неравенство, но(!), поскольку нам нужно минимизировать количество отчетных периодов, то необходимо стремиться, как можно быстрее закрыть кредит, а для этого нужно выплачивать транши максимального размера. Следовательно, принимаем, что самый $1$-ый платеж составляет ровно $1.8$ миллионов рублей.
Перед тем, как осуществить первую выплату $(i = 1)$, банк начисляет проценты на текущее тело кредита.
$\%_ = S * r$ - сумма начисленных процентов, млн.рублей.
Сейчас нам нужно понять, чему равна одна часть первоначального кредита. Поскольку в модели дифференцируемых платежей тело кредита уменьшается равномерно, значит одна часть> = $\frac$ или $=\frac * S$.
Соберем все составляющие воедино и запишем формулу, по которой можно получить размер $1$-го платежа:
$p_ = \%_ + \frac = S * r + \frac = S * (r + \frac)$.
Чуть выше мы уже доказали, чему должен быть равен $1$-й платеж, поэтому составим и решим следующее уравнение:
Готово! Ответ получен! Чтобы соответствовать всем условиям и ограничениям, озвученным в условии задачи, необходимо взять кредит сроком, ровно на $10$ лет.
На своих частных уроках, совместно с учеником, мы проводим верификацию полученных результатов, посредством математического процессора "MS Excel". Это позволяет убедиться в правильности полученного решения, а также лишний раз проанализировать математические выкладки, участвующие в процессе дифференцируемых платежей. Это очень полезное занятие!

Сформированная в MS Excel таблица, доказывает правильность нашего алгебраического решения.
Ответ: 10.
Выводы
Некоторые задачи на модель дифференцируемых платежей можно решить буквально за $1-2$ минуты, если фундаментально понимать математическую модель этого типа платежей.
Обращайте особое внимание на ограничения в условии задачи, так как именно они позволяют резко упростить математические выкладки. И, как правило, решение становится предельно простым и быстро получаемым.
Зазубрите свойства схемы дифференцированных платежей. Это позволит вам почти моментально определять вектор последующего математического решения. В данном примере мы использовали свойство дифференцированных выплат, проявляющееся в том, что самый $1$-й платеж является и самым наибольшим.
Старайтесь решать экономические задачи алгебраическим способом, когда нужно сформировать какие-либо уравнения/неравенства, а не арифметическим. Арифметический способ решения требует наличия громоздких вычислений, и, как правило, является крайне времязатратным.
И, пожалуй, одно из главных - нужно любить математику.
Примеры условий реальных задач, встречающихся на ЕГЭ по математике
В данном разделе я приведу лишь условия некоторого количества задач, которые наиболее часто встречаются на официальном экзамене ЕГЭ по математике. В каждой из задач акцентировано внимание на модели дифференцируемого платежа, и только на нем.
А ведь существует масса комбинированных финансовых задач, в процессе решения которых дифференцируемый платеж занимает лишь какую-то часть решения. Все подобные задачи я разбираю со своими учениками на индивидуальных занятиях.
Пример №1
В мае планируется взять кредит в банке на сумму \(10\) миллионов рублей на \(5\) лет.
Условия его возврата таковы:
Каждый декабрь долг возрастает на \(10\%\) по сравнению с концом предыдущего года.
С января по март каждого года необходимо выплатить часть долга.
В мае каждого года долг должен быть на одну и ту же величину меньше долга на май предыдущего года.
Сколько миллионов рублей составила общая сумма выплат после погашения банковского кредита?
Пример №2
В июле планируется взять кредит в банке на сумму \(6\) миллионов рублей на некоторый срок.
Условия его возврата таковы:
Каждый январь долг возрастает на \(20\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил \(1.8\) миллиона рублей?
Пример №3
В июле планируется взять кредит в банке на сумму \(20\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(30\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(47\) миллионов рублей?
Пример №4
В июле планируется взять кредит в банке на сумму \(16\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(25\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(38\) миллионов рублей?
Пример №5
В июле планируется взять кредит в банке на сумму \(6\) миллионов рублей на срок \(15\) лет.
Условия его возврата таковы:
Каждый январь долг возрастает на \(q\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найти \(q\), если известно, что наибольший годовой платеж по кредиту составит не более \(1.9\) миллиона рублей, а наименьший не менее \(0.5\) миллиона рублей.
Пример №6
\(15\) января планируется взять кредит в банке на \(39\) месяцев.
Условия его возврата таковы:
\(1-го\) числа каждого месяца долг возрастает на \(q\%\) по сравнению с концом предыдущего месяца.
Со \(2-го\) по \(14-е\) число месяца необходимо выплатить часть долга.
\(15-го\) числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на \(15-е\) число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на \(20\%\) больше суммы, взятой в кредит. Найдите \(q\).
Пример №7
Анатолий взял банковский кредит сроком на \(9\) лет. В конце каждого года общая сумма оставшегося долга увеличивается на \(17\%\), а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого года, подбираются так, чтобы в результате сумма долга каждый год уменьшалась равномерно, то есть на одну и ту же величину.
Сколько процентов от суммы кредита составила общая сумма, уплаченная Анатолием банку (сверх кредита)?
Пример №8
Анна взяла кредит в банке на срок \(12\) месяцев (\(1\) календарный год). В соответствии с банковским договором Анна возвращает кредит банку ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется \(q\%\) этой суммы, и своим ежемесячным платежом Анна погашает эти добавленные проценты и уменьшает сумму долга.
Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая модель называется "схемой с дифференцированными платежами"). Известно, что общая сумма, выплаченная Анной банку за весь период кредитования, оказалась на \(13\%\) больше, чем сумма, взятая ей в кредит. Найдите процентную ставку банка, то есть \(q\).
Пример №9
В июле планируется взять кредит в банке на сумму \(28\) миллионов рублей на некоторый срок (целое число лет).
Условия его возврата таковы:
Каждый январь долг возрастает на \(25\%\) по сравнению с концом предыдущего года.
С февраля по июнь каждого года необходимо выплатить часть долга.
В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит \(9\) миллионов рублей?
Пример №10
\(15\) января планируется взять кредит в банке на \(15\) месяцев.
Условия его возврата таковы:
\(1-го\) числа каждого месяца долг возрастает на \(1\%\) по сравнению с концом предыдущего месяца.
Со \(2-го\) по \(14-е\) число каждого месяца необходимо выплатить часть долга.
\(15-го\) числа каждого месяца долг должен быть на одну и ту же величину меньше долга на \(15-е\) число предыдущего месяца.
Известно, что восьмая выплата составила \(108\,000\) рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Не удивляйтесь, но приведенные задачи решаются достаточно легко, если у вас присутствует детальнейшее понимание анатомии дифференцируемого платежа. Даже скажу больше, ответы на некоторые из представленных мною задач можно посчитать в уме, не прибегая к каким-либо записям и вычислениям на бумаге/компьютере.
Хотите научиться безошибочно решать подобный класс упражнений из экономического блока ЕГЭ по математике? Тогда записывайтесь ко мне на индивидуальную подготовку! Я – репетитор-практик с многолетним стажем, и главная цель моих занятий – выработать у вас навыки успешного решения экономических задач любого типа и любой сложности.
Что-то все равно осталось непонятным? Записывайтесь ко мне на частную подготовку!
Да, я прекрасно знаю разницу, когда производишь решение самостоятельно, и, когда знакомишься с уже готовым решением. В данной статье я демонстрирую профессиональное решение одной из множества задач на дифференцируемый платеж. Вам далеко не все может быть понятно!
По-настоящему научиться решать экономические задачи можно лишь тогда, когда прорешиваешь их самостоятельно или работаешь под началом какого-либо репетитора/наставника. Достаточно сложно стать профессиональным математическим решателем, если постоянно анализировать только чужие решения.
Поэтому, если хотите стать намного сильнее в области финансовой математики, получать в качестве домашних заданий сложные примеры, требующие нестандартного подхода, то записывайтесь ко мне на частные уроки.
На своих частных уроках я делаю упор исключительно на практические решения. Мы не занимаемся водянистой теорией, которая легкодоступна на множестве информационных ресурсов сети Интернет.
И не стоит забывать о том, что я достаточно востребованный репетитор. Поэтому не откладывайте свое решение в долгий ящик, а действуйте прямо сейчас! Звоните по номеру, указанному в шапке данного сайта, или пишите мне на электронный адрес (ссылку можно найти в подвале сайта в разделе "Контакты").
Экономические задачи достаточно интересны по своей природе, а также понимание их решения может вам пригодиться в реальной жизни. Кто знает, может быть, вы будущий экономист или трейдер на финансовых рынках.
В июне планируется взять кредит в банке на сумму 455 000 рублей на некоторый срок (целое число лет). Условия его возврата таковы:
- каждый год в январе месяце долг повышается на 20% по сравнению с концом прошлого года;
- с февраля по май каждого года требуется выплатить часть долга;
- ежегодные выплаты составляют одну и ту же постоянную величину.
На сколько лет берется кредит, если известно, что общая сумма выплат по кредиту после его полного погашения составит 648 000 рублей?
Решение
k=455 тыс. рублей — сумма кредита,
x тыс. рублей — сумма ежегодного платежа,
n — число лет, на которые планируется взять кредит.
Из условия следует таблица:
| Год | Платеж | Остаток |
| 1 | x | 1,2k-x |
| 2 | x | 1,2(1,2k-x)-x=1,2^2k-1,2x-x |
| 3 | x | 1,2(1,2^2k-1,2x-x)-x=1,2^3k-1,2^2x-1,2x-x |
| . | . | . |
| n | x | 1,2^nk-1,2^x-. -1,2x-x |
Из этой таблицы и условия задачи следует система уравнений:
Второе уравнение этой системы можно записать в виде
Так как 1,2^+1,2^+. +1,2+1 — сумма первых n членов геометрической прогрессии с первым членом 1 и знаменателем 1,2 , то 1,2^+1,2^+. +1,2+1= \frac= \frac.
Тогда, учитывая, что x=\frac из первого уравнения системы, для второго уравнения получим:
Перепишем последнее уравнение в виде
6^n-5^n=7 \cdot 13 \cdot n \cdot 2^ \cdot 3^.
Так как справа от знака равенства должно быть целое число, то n \geq 3.
Перебором находим единственный целый корень уравнения n=3.
Можно ограничить n , если использовать свойства делимости. Выразим n из последнего уравнения:
Это натуральное число, значит, число множителей 2 в знаменателе не больше числа множителей 2 в числителе, то есть n \leq3.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задача 17 – одна из сложных задач ЕГЭ. Они делятся на “экономические” и “неэкономические”. В первых, как правило, нужно уметь определять срок кредитования, сумму кредита, банковский процент или величину платежа.
Задача 1. В июле планируется взять кредит в банке на сумму 6 млн рублей на некоторый срок.
Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На какой минимальный срок следует брать кредит, чтобы наибольший годовой платеж по кредиту не превысил 1,8 млн рублей?
Снова мы столкнулись с условием, когда долг должен быть меньше долга на предыдущий период времени на одну и ту же величину. Это означает, что платежи не будут равными, потому что в каждый из платежей необходимо выплатить все проценты, начисленные банком до того, и еще часть суммы самого кредита. Поэтому при такой схеме первый платеж является самым крупным (проценты начисляются на целую, еще не уменьшенную нами, сумму кредита), а последний – самым маленьким.
В нашем случае процент известен, поэтому в первый платеж надо будет выплатить процент: $X \cdot \frac= 6 \cdot \frac$, да еще неизвестную часть кредита: $\frac=\frac$, и по условию эта сумма не должна быть больше 1,8 млн. Поэтому
Задача 2. В июле планируется взять кредит в банке на сумму 20 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 47 млн рублей?
Задача с похожим условием. Давайте разбираться. Как мы выяснили ранее (например, в предыдущей задаче), платежи равными не будут. Самый большой платеж – первый, а потом каждый последующий все меньше и меньше, потому что с каждым платежом долг уменьшается на одну и ту же величину и процент, следовательно, тоже.
Сначала банк начислит нам процент на всю сумму кредита: $X \cdot \frac$, но в первый же платеж мы выплатим все эти деньги и вернем еще и часть долга, равную $\frac$. Тогда мы останемся должны $X-\frac=\frac$, и уже на эту сумму банк нам начислит проценты. И так далее: выплачиваем проценты и часть долга, банк начисляет проценты на оставшуюся часть.
Тогда в конце концов мы выплатим банку весь долг – 20 млн – и всю сумму процентов, всего – 47 млн, а сумма процентов будет ни что иное, как арифметическая прогрессия:
Членов у такой прогрессии ровно столько, на сколько лет (ну или месяцев – где как) взят кредит, разность такой прогрессии равна $d=-\frac$, первый член – полная сумма, взятая в долг. Сумма арифметической прогрессии в скобках равна
В нашем случае сумма процентов равна $47-20=27$ млн, поэтому
Задача 3. В июле планируется взять кредит в банке на сумму 16 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 40 млн рублей?
Задача точно такая же, но с другими цифрами. Формулу больше не выводим, а просто ею пользуемся. Переплата равна:
Задача 4. В июле планируется взять кредит в банке на сумму 1 300 000 рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
На какое минимально количество лет можно взять кредит при условии, что ежегодные выплаты были не более 350 000 рублей?
Если бы не проценты, мы вернули бы банку долг приблизительно за 4 года: $ \frac=3,7$ . Самая большая сумма процентов – первая – равна $P=0,1\cdot1300000=130000$, остальные будут меньше. Тогда, если умножить эту сумму на 4, получим, что проценты (по максимуму) составят $4\cdot130000=520000$. Так как
то за пять лет точно справимся (помним, что проценты будут меньше с каждым платежом, сумма в 520000 сильно завышена).
Можно решать задачу по-иному, а именно, табличным способом. Необходимо просто рассчитать все платежи и начисления.
Первый год: начисляем проценты.
Второй год. Начисляем проценты:
Третий год. Начисляем проценты:
Четвертый год. Начисляем проценты:
Таким образом, выплата пятого года оказывается последней.
Задача 5. 1 января 2015 года Александр Сергеевич взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая: 1-го числа каждого месяца банк начисляет 1 % на оставшуюся сумму долга (то есть увеличивает долг на 1 %), затем Александр Сергеевич переводит в банк платеж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?
Самый большой платеж – первый – равен сумме процентов $X \cdot \frac= 1 100 000 \cdot \frac$ и части долга¸ равной $\frac=\frac$, и по условию эта сумма не должна быть больше 275 000. Поэтому
$$1 100 000 \cdot \frac +\frac=275 000$$
Иными словами, Александр Сергеевич не сможет расплатиться за 4 месяца, поэтому минимальный срок – 5 месяцев.
Задачу можно решать и так: $275 000 \cdot n=1 100 000$ – то есть $n=4$ при условии, что не надо выплачивать проценты. Наибольшую сумму процентов – $X \cdot \frac= 1 100 000 \cdot \frac=11 000$ – Александру Сергеевичу предстоит выплатить в первый платеж, потом они будут уже меньше. То есть максимальная сумма выплат (без учета того, что проценты уменьшаются, то есть с лихвой) равна $1 100 000 + 11 000\cdot 5=1 155 000$, а $275 000 \cdot 5=1 375 000$ – то есть за 5 месяцев он всяко сможет расплатиться.
Ответ: 5 месяцев
Один из типов экономических задач — это задачи на платежи с равномерно убывающим долгом. Каждый месяц (период) основной долг уменьшается на одинаковую сумму. Ежемесячный платёж будет состоять из суммы основного долга и суммы начисленных процентов на остаток долга.
В этом случае мы имеем дело с дифференцированными платежами.
Внимание: в задачах этого типа применяется формула суммы n-первых членов арифметической прогрессии.
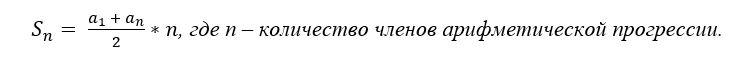
Задачи для разбора берутся из вариантов ЕГЭ прошлых лет, размещённых на популярном среди школьников и учителей сайте РЕШУ ЕГЭ .
Задача 1. Рассчитать сумму кредита
15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:
-
1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
Какую сумму следует взять в кредит, чтобы общая сумма выплат по кредиту после полного его погашения составила 2 млн руб. (никакие округления при вычислении платежей не производятся)?
S тыс. руб. — сумма кредита,
2 млн руб. = 2000 тыс. руб.,
X тыс. руб. — ежемесячная выплата основного долга.
Суммы ежемесячного долга: S; (S — X); (S — 2 * X . S — 47 * X); (S — 48 * X); 0
S * p; (S — X) * p; (S — 2 * X) * p . (S — 47 * X) * p; (S — 48 * X) * p; 0
Сумма выплат = Сумма кредита + Проценты

S * (1 + 49 * p — 24 * p) = 2000
S * (1 + 25 * 0,01) = 2000
S = 1600 тыс. руб., или 1,6 млн руб.
Ответ: 1,6 млн руб.
Задача 2. Рассчитать сумму кредита
15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
-
1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1,604 млн руб. (1604 тыс. руб.)?
Задача отличается от предыдущей — выплаты по основному долгу (30 тыс. руб.) осуществляются только первые 20 месяцев, а значит, в последний месяц выплата будет иной.
S тыс. руб. — сумма кредита
Суммы ежемесячного долга: S; (S — 30); (S — 60. S — 570); (S — 600); 0
Начисленные проценты: S * р; (S — 30) * р; (S — 60) * р. (S — 570) * р; (S — 600) * р; 0
Сумма выплат = Сумма кредита + Проценты


S * (1 + 21 * 0,03) — 0,03 * 6300 = 1604
1,63 * S — 189 = 1604
1,63 * S = 1604 + 189
S = 1100 тыс. руб., или 1,1 млн руб.
Ответ: 1,1 млн руб.
Задача 3. Рассчитать, на сколько месяцев планируется взять кредит
15 января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условия его выплаты таковы:
-
1-го числа n-ого месяца долг возрастёт на 3% по сравнению с концом предыдущего месяца;
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?

Превышение выплат на 30% от суммы кредита — за счёт выплаченных процентов.
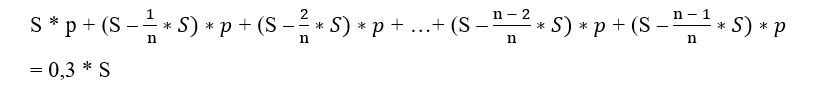
Раскрываем скобки и группируем слагаемые.

Ответ: 19 месяцев.
Еженедельная рассылка с лучшими материалами «Открытого журнала»
Без минимальной суммы, платы за обслуживание и скрытых комиссий
Для оформления продукта необходим брокерский счёт
проект «Открытие Инвестиции»
Открыть брокерский счёт
Тренировка на учебном счёте
Об «Открытие Инвестиции»
Москва, ул. Летниковская,
д. 2, стр. 4
8 800 500 99 66
Согласие на обработку персональных данных
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Экономические задачи ввели в единый государственный экзамен по математике (профильный уровень) с 2015 года. При их решении у экзаменующихся часто возникают затруднения, ведь в жизни они пока не сталкивались с кредитами и вкладами, а значит, плохо понимают условия задач и действия, выполняемые внутри них.
Разбор типовых задач (задание 17) из ЕГЭ по математике профильного уровня будет полезен не только выпускникам школ, но и любителям прикладных методов в банковской сфере.
Как решать экономические задачи?
Часть экономических задач можно решить универсальным способом — с помощью составления таблицы, которая позволит упорядочить данные по временным интервалам.
Для всех типов задач при составлении таблицы используется единый алгоритм.

Условия задач взяты с сайта РЕШУ ЕГЭ .
Задачи на равные платежи по кредиту
В задачах этого типа заёмщик всегда вносит равные суммы. При решении подобных задач надо следовать ряду советов.
-
Не торопитесь сразу в ходе решения использовать числовые данные задачи. Решите задачу в общем виде.
Задача 1. Рассчитываем общую сумму кредита
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
-
каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;
Какая сумма была взята в банке, если известно, что кредит был полностью погашен тремя равными платежами (то есть за три года)?
S руб. — сумма кредита,
р = 0,31,
r = 131,
В = 69 690 821 руб. — ежегодная выплата.
| Долг с начисленными процентами | Выплата | Остаток долга | |
| 1 | S * r | B | S * r — B |
| 2 | (S * r — B) * r | B | (S * r — B) * r — B |
| 3 | ((S * r — B) * r — B) * r | B | 0 |
По последней строке составляем уравнение:

Далее последовательно раскроем скобки:

Теперь можно подставить числовые данные:

Многолетняя практика по решению реальных экзаменационных вариантов показывает, что числовые данные для задач подбираются неслучайно. Составители могут специально подбирать значения таким образом, чтобы получающиеся при вычислениях дроби можно было сократить. Поэтому, прежде чем взяться за вычисление знаменателя, надо проверить, будет ли число 69 690 821 делиться на 1,31.

Ответ: Общая сумма кредита 124 809 100 руб.
Задача 2. Рассчитываем процент кредита
31 декабря 2020 г. Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на х%), затем Пётр переводит очередной платёж. Если он будет платить каждый год по 2 592 000 руб., то выплатит долг за четыре года. Если по 4 392 000 руб., то за два года. Под какой процент Пётр взял деньги в банке?
S тыс. руб. — сумма кредита,
Х% — в десятичной дроби,
r = 1 + a,
А = 2 592 000 руб. — ежегодный платёж 1,
В = 4 392 000 руб. — ежегодный платёж 2.
| Долг с начисленными процентами | Выплата | Остаток долга | |
| 1 | S * r | А | S * r — А |
| 2 | (S * r — А) * r | А | (S * r — А) * r — А |
| 3 | ((S * r — А) * r — А) * r | А | ((S * r — А) * r — А) * r — А |
| 4 | (((S * r — А) * r — А) * r — A) * r | А | 0 |
| 1 | S * r | B | S * r — B |
| 2 | (S * r — B) * r | B | 0 |
Из таблицы видно, что последнее начисление банка при каждой схеме выплат равно ежегодной выплате.
Получаем систему уравнений:

Помните о культуре вычислений и об отсутствии калькулятора.
Выражаем S из каждого уравнения:


Теперь подставляем числовые значения:

Значит, а = 1,2 — 1 = 0,2, или 20%
Ответ: Пётр взял кредит под 20%.
О чём необходимо помнить при решении экономических задач
Старайтесь предварительно упрощать выражения, используя алгебраические преобразования.
Мы разобрали алгоритм решения задач с использованием таблицы, но возможны и другие способы решений.
Еженедельная рассылка с лучшими материалами «Открытого журнала»
Без минимальной суммы, платы за обслуживание и скрытых комиссий
Для оформления продукта необходим брокерский счёт
проект «Открытие Инвестиции»
Открыть брокерский счёт
Тренировка на учебном счёте
Об «Открытие Инвестиции»
Москва, ул. Летниковская,
д. 2, стр. 4
8 800 500 99 66
Согласие на обработку персональных данных
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Автор статьи

Читайте также:

