15 декабря планируется взять кредит в банке на 31 месяц условия его возврата таковы
Обновлено: 26.07.2024
Задачи на кредиты по схемам научились уже решать буквально все. Кто-то понял схему, «прочувствовал» ее, кто-то выучил порядок действий. Поэтому на экзамене ЕГЭ сейчас задач, решаемых по схемам (дифференцированного платежа или аннуитета) уже и не встретишь. Обязательно или присутствуют обе схемы, или схема нарушена. Сейчас стали актуальными задачи именно с нарушенной схемой. Поэтому я предлагаю целую серию задач, после решения которых вы поймете, что вам по плечу ЛЮБАЯ экономическая задача. Обещаю, что если вы одолеете эту серию статей, то решать 17-е задачи вы будете буквально «на щелк пальцами». Задачи авторские: автор Ирина Евгеньевна Самохина.
Задача 5. 15 декабря планируется взять кредит в банке на $S$ тыс. рублей на 32 месяца. Условия его возврата таковы:
– 1 числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2 по 14 число каждого месяца необходимо выплатить часть долга;
– 15 числа первый и последний месяцы долг должен уменьшиться на 250 тыс. рублей, все остальные месяцы долг должен быть меньше долга на 15 число предыдущего месяца на $a$ тысяч рублей.
Найдите $S$, если всего было выплачено банку 2061,5 тыс. рублей.
Составим таблицу. В первом столбце будет сумма, которую мы должны банку, во втором – начисленные на нее проценты, в третьем – платеж этого месяца.

Так как нам известна сумма всех выплат банку, то нужно собрать вместе все платежи, то есть сложить все суммы последнего столбца. Тогда
$$2\cdot 250+5+n\cdot a+0,02\left(S+S-250+S-250-a+S-250-2a+…S-250-29a\right)=2061,5$$
Заметим, что мы выплатили банку два раза по 250 тыс и $n$ раз по $a$. То есть произведение $na=S-500$ тыс. Тогда
Ответ: $S=1550$ тыс.
Задача 6. 15 декабря планируется взять кредит в банке на $2400$ тыс. рублей на ($n+2$) месяца. Условия его возврата таковы:
– 1 числа каждого месяца долг возрастает на 2,5 % по сравнению с концом предыдущего месяца;
– со 2 по 14 число каждого месяца необходимо выплатить часть долга;
– 15 числа первый и последний месяцы долг должен уменьшиться на $400$ тыс. рублей, все остальные месяцы долг должен быть меньше долга на 15 число предыдущего месяца на $a$ тысяч рублей.
Найдите $n$, если всего было выплачено банку 3690 тыс. рублей.
Составим таблицу. В первом столбце будет сумма, которую мы должны банку, во втором – начисленные на нее проценты, в третьем – платеж этого месяца.

Так как нам известна сумма всех выплат банку, то нужно собрать вместе все платежи, то есть сложить все суммы последнего столбца. Тогда
$$2\cdot 400+10+n\cdot a+0,025\left(S+S-400+S-400-a+S-400-2a+…S-400-(n-1)a\right)=3690$$
Заметим, что мы выплатили банку два раза по 400 тыс и $n$ раз по $a$. То есть произведение $na=S-800=1600$ тыс. Тогда

Задание 15 № 520941
15-го декабря планируется взять кредит в банке на сумму 1100 тысяч рублей на 31 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 31-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 30-го месяца, если общая сумма выплат после полного погашения кредита составит 1503 тысячи рублей?
Пусть 15-го числа 30-го месяца долг составит B тысяч рублей. По условию, долг перед банком (в тыс. рублей) по состоянию на 15-е число должен уменьшаться до нуля следующим образом:
Первого числа каждого месяца долг возрастает на 2%, значит, последовательность размеров долга (в тыс. рублей) по состоянию на 1-е число такова:
Следовательно, выплаты (в тыс. рублей) должны быть следующими:
Всего следует выплатить откуда
Значит, 15-го числа 30-го месяца долг составит 200 тыс. рублей.
Ответ: 200 000 руб.
Аналоги к заданию № 520872: 520941 520948 Все
Здравствуйте, почему мы при уменьшении долга добавляем к каждому числу долг 30-го месяца? Что-то не корректно получается
Если 15-го числа 30-го месяца долг составит B, значит каждый месяц долг уменьшается на .
Значит 15-го числа 1-го месяца долг составит

Задание 15 № 520948
15-го декабря планируется взять кредит в банке на сумму 1 000 000 рублей на 11 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 10-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 11-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 10-го месяца, если общая сумма выплат после полного погашения кредита составит 1231 тысячи рублей?
Пусть 15-го числа 10-го месяца долг составит B тысяч рублей. По условию, долг перед банком (в тыс. рублей) по состоянию на 15-е число должен уменьшаться до нуля следующим образом:
Первого числа каждого месяца долг возрастает на 3%, значит, последовательность размеров долга (в тыс. рублей) по состоянию на 1-е число такова:
15-го декабря планируется взять кредит в банке на сумму 1100 тысяч рублей на 31 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 31-го месяца кредит должен быть полностью погашен. Какой долг будет 15-го числа 30-го месяца, если общая сумма выплат после полного погашения кредита составит 1503 тысячи рублей?
Решение


Откуда 660 взялись?
Слагаемое 22 повторяется 30 раз - это 22*30=660
Все решения
Кредит на [b]31 месяц[/b]
1)[i] условие [/i]
–1–го числа каждого месяца долг увеличивается на 2% по сравнению с концом предыдущего месяца
См первый столбик ( начисление процентов на долг)
2) [i]условие [/i]
– со 2го по 14–е число каждого месяца необходимо [b]выплатить одним платежом часть долга;[/b]
[red]и так, чтобы
выполнялось условие [/red]
3)[i] условие [/i]
15–го числа каждого месяца с 1–го по 30–й месяц ( 30 раз) долг должен быть [b]на одну и ту же сумму меньше долга [/b]на 15–е число [b]предыдущего месяца;[/b]
Это показано в правом столбце таблицы
к 15–му числу 31–го месяца кредит должен быть полностью погашен.
Поэтому остаток 30-го месяца неизвестен. Пусть он равен B
С него и начинаем решать задачу, так называемым [i]"методом решения задачи с конца" [/i]
Пусть долг ежемесячно уменьшается на одну и ту же величину[b] х тыс руб[/b]
[/b] сумма кредита составляет [b](B+30х)тыс руб[/b]
В первом столбце показано как начисляют проценты.
[b]Проценты начисляют на остаток долга[/b]
Поэтому за [b] 1-ый месяц проценты[/b] начислены на весь кредит.
1%=0,02
0,02*(B+30х) - % , начисленные за первый месяц
[b]Клиент выплачивает[/b] со второго по 14 число первого месяца ( одним платежом)
проценты и часть кредита х тыс руб:
0,02*(B+30х) + [b]x [/b]
Остаток долга на х меньше и равен (B+30x)-x=B+29x
Остаток долга уменьшится на х тыс. руб.
[b]Цикл повторяется 30 раз[/b]
Таким образом, останов к концу 30 месяца равен В тыс. руб
1 числа 31-го месяца начисляют проценты на этот остаток. Клиент выплачивает проценты на остаток 30-го месяца и сам остаток:
0,02*B + B
Один из типов экономических задач — это задачи на платежи с равномерно убывающим долгом. Каждый месяц (период) основной долг уменьшается на одинаковую сумму. Ежемесячный платёж будет состоять из суммы основного долга и суммы начисленных процентов на остаток долга.
В этом случае мы имеем дело с дифференцированными платежами.
Внимание: в задачах этого типа применяется формула суммы n-первых членов арифметической прогрессии.
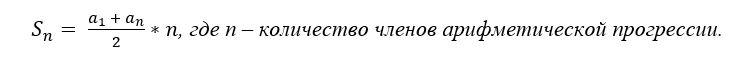
Задачи для разбора берутся из вариантов ЕГЭ прошлых лет, размещённых на популярном среди школьников и учителей сайте РЕШУ ЕГЭ .
Задача 1. Рассчитать сумму кредита
15 января планируется взять кредит в банке на 49 месяцев. Условия его возврата таковы:
-
1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
Какую сумму следует взять в кредит, чтобы общая сумма выплат по кредиту после полного его погашения составила 2 млн руб. (никакие округления при вычислении платежей не производятся)?
S тыс. руб. — сумма кредита,
2 млн руб. = 2000 тыс. руб.,
X тыс. руб. — ежемесячная выплата основного долга.
Суммы ежемесячного долга: S; (S — X); (S — 2 * X . S — 47 * X); (S — 48 * X); 0
S * p; (S — X) * p; (S — 2 * X) * p . (S — 47 * X) * p; (S — 48 * X) * p; 0
Сумма выплат = Сумма кредита + Проценты

S * (1 + 49 * p — 24 * p) = 2000
S * (1 + 25 * 0,01) = 2000
S = 1600 тыс. руб., или 1,6 млн руб.
Ответ: 1,6 млн руб.
Задача 2. Рассчитать сумму кредита
15 декабря планируется взять кредит в банке на 21 месяц. Условия возврата таковы:
-
1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1,604 млн руб. (1604 тыс. руб.)?
Задача отличается от предыдущей — выплаты по основному долгу (30 тыс. руб.) осуществляются только первые 20 месяцев, а значит, в последний месяц выплата будет иной.
S тыс. руб. — сумма кредита
Суммы ежемесячного долга: S; (S — 30); (S — 60. S — 570); (S — 600); 0
Начисленные проценты: S * р; (S — 30) * р; (S — 60) * р. (S — 570) * р; (S — 600) * р; 0
Сумма выплат = Сумма кредита + Проценты


S * (1 + 21 * 0,03) — 0,03 * 6300 = 1604
1,63 * S — 189 = 1604
1,63 * S = 1604 + 189
S = 1100 тыс. руб., или 1,1 млн руб.
Ответ: 1,1 млн руб.
Задача 3. Рассчитать, на сколько месяцев планируется взять кредит
15 января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условия его выплаты таковы:
-
1-го числа n-ого месяца долг возрастёт на 3% по сравнению с концом предыдущего месяца;
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит?

Превышение выплат на 30% от суммы кредита — за счёт выплаченных процентов.
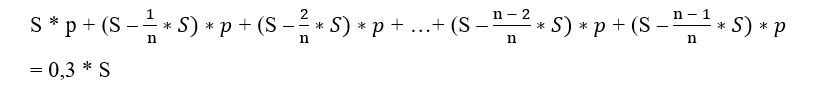
Раскрываем скобки и группируем слагаемые.

Ответ: 19 месяцев.
Еженедельная рассылка с лучшими материалами «Открытого журнала»
Без минимальной суммы, платы за обслуживание и скрытых комиссий
Для оформления продукта необходим брокерский счёт
проект «Открытие Инвестиции»
Открыть брокерский счёт
Тренировка на учебном счёте
Об «Открытие Инвестиции»
Москва, ул. Летниковская,
д. 2, стр. 4
8 800 500 99 66
Согласие на обработку персональных данных
Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
15 января планируется взять кредит в банке на некоторую сумму на 31 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на \(1\%\) по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить одним платежом часть долга;
— на 15-ое число каждого месяца с 1-го по 30-й долг должен должен быть на 20 тыс. рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 31-го месяца долг должен быть погашен полностью.
Сколько тысяч рублей составляет долг на 15 число 30-ого месяца, если банку всего было выплачено 1348 тыс. рублей?
(ЕГЭ 2018, основная волна)
Пусть в банке взято \(A\) тыс. рублей. Заметим, что фраза “на 15 число каждого с 1 по 30 месяц долг должен уменьшаться на 20 тыс. руб.” означает, что с 1 по 30 месяц долг выплачивался дифференцированными платежами, то есть сначала гасились начисленные проценты, а затем вносилась одна и та же сумма, равная 20 тыс. рублей, вследствие чего после платежей с 1 по 30 месяц долг менялся так:
\(A-20 \ \rightarrow\ A-2\cdot 20 \ \rightarrow \ A-3\cdot 20 \ \rightarrow \dots \ \rightarrow \ A-30\cdot 20\) .
Так как в 31 месяце долг должен быть погашен полностью, то это значит, что платеж в 31 месяце будет равен оставшемуся долгу (после начисления процентов).
Составим таблицу, в которой все будет выглядеть более наглядно: \[\begin <|l|l|l|l|l|>\hline \text & \text\% & \text\% &\text & \text\\ &&&&\text\\ \hline 1 & A&A+0,01 A &0,01A+20 &A-20\\ \hline 2 & A-20& (A-20)+0,01(A-20)&0,01(A-20)+20 &A-40\\ \hline 3 & A-40& (A-40)+0,01(A-40)&0,01(A-40)+20 &A-60\\ \hline \dots &\dots &\dots &\dots &\dots \\ \hline 30 & A-580& (A-580)+0,01(A-580)&0,01(A-580)+20 &A-600\\ \hline 31 & A-600& 1,01(A-600)&1,01(A-600) &0\\ \hline \end\]
Исходя из условия задачи, нужно найти \(A-600\) . Для этого нужно найти \(A\) . Так как всего было выплачено банку 1348 тыс. рублей, то сумма всех выплат равна 1348 тыс. рублей:
\((0,01A+20)+ (0,01(A-20)+20 )+(0,01(A-40)+20 )+\dots +(0,01(A-580)+20) +(1,01(A-600) )=1348\)
Таким образом, ответ: \(A-600=500\) .
15-ого апреля планируется взять кредит в банке на 700 тысяч рублей на \((n+1)\) месяц. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на \(1\%\) по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить одним платежом часть долга;
– 15-го числа каждого с 1-го по \(n\) -ый месяц долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
– 15-го числа \(n\) -го месяца долг составлял 300 тысяч рублей;
– к 15-му числу \((n+1)\) -го месяца долг должен быть погашен полностью.
Найдите \(n\) , если банку всего было выплачено 755 тысяч рублей.
(ЕГЭ 2018, основная волна)
Фраза “15-го числа каждого с 1-го по \(n\) -ый месяц долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца” означает, что долг каждый месяц после выплаты уменьшался на одну и ту же сумму (неизвестную, поэтому обозначим ее за \(x\) тыс. руб.), следовательно, сначала долг составлял 700 тыс. руб., затем после первой выплаты он составил \(700-x\) тыс. руб., после второй – \(700-2x\) тыс. руб. и т.д. Таким образом, после \(n\) -ой выплаты долг должен быть равен \(700-nx\) тыс. рублей.
Заметим, что долг после первой выплаты равен долгу в начале второго месяца, следовательно, долг после \(n\) -ой выплаты равен долгу на начало \((n+1)\) -го месяца. Следовательно, из условия задачи находим, что \(700-nx=300\) .
За \((n+1)\) -ый месяц долг должен быть выплачен полностью.
Составим наглядную таблицу. Чтобы удобнее было записывать выплаты с 1 по \(n\) -ый месяцы, долг после начисления процентов будем записывать в виде “долг + начисленные проценты”: \[\begin <|l|l|l|l|>\hline \text &\text\% &\text\% &\text\\ \hline 1 & 700 & 700 + 0,01\cdot 700 &0,01\cdot 700+x\\ \hline 2 & 700-x & 700-x +0,01(700-x) & 0,01(700-x)+x\\ \hline 3 & 700-2x & 700-2x+0,01(700-2x) & 0,01(700-2x)+x\\ \hline \dots &\dots &\dots &\dots \\ \hline n & 700-(n-1)x &700-(n-1)x +0,01(700-(n-1)x) & 0,01(700-(n-1)x)+x\\ \hline n+1 & 700-nx=300 & 1,01 (700-nx)=303 & 1,01 (700-nx)=303 \\ \hline \end\]
Чтобы найти сумму, которая была в итоге выплачена банку, нужно сложить все платежи. Следовательно,
\(\left(0,01\cdot 700+x\right) + \left(0,01(700-x)+x\right) + \left(0,01(700-2x)+x\right) + \dots +\left(0,01(700-(n-1)x)+x\right)+303=755\)
Первые \(n\) слагаемых образуют арифметическую прогрессию (с разностью \(0,01x\) ). Следовательно, их сумму можно вычислить по формуле \(S_n=\dfrac2\cdot n\) : \[\dfrac2\cdot n=452\] Преобразуем левую часть полученного равенства (из равенства \(700-nx=300\) найдем \(nx=400\) ): \[\begin &\dfrac2\cdot n=\\[2ex] &=(0,01\cdot 700+x-0,005(n-1)x)n=\\[2ex] &=(7+x-0,005nx+0,005x)n=\text< (так как >nx=400)\\[2ex] &=(7+x-2+0,005x)n=5n+xn+0,005xn=5n+400+2=5n+402 \end\] Таким образом, мы получаем уравнение \[5n+402=452\quad\Rightarrow\quad n=10\]
Автор статьи

Читайте также:

