Предприятие получило в коммерческом банке кредит на сумму 126 млн рублей сроком на 3 года

Обновлено: 08.05.2024

Встречаются задачи, в которых долг по кредиту уменьшается неравномерно, а убывает согласно данным, представленным в таблице.

Задачи для разбора взяты с сайта РЕШУ ЕГЭ .

Задача 1. Рассчитываем разницу между общей суммой выплат и суммой самого кредита

15 января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

При решении данной задачи воспользуемся советами, данными в прошлой статье «Проценты по кредиту с равными платежами».

Учитываем, что общая сумма выплат будет превышать сумму кредита за счёт начисленных и уплаченных процентов.

I способ — решим задачу в общем виде, приняв за сумму кредита S руб. р = 5% = 0,05,

Представим решение в виде таблицы.

Долг с начисленными процентами, руб.	Выплата, руб.	Остаток долга, руб.	Остаток долга, %
Февраль	Sr	Sr — 0,9S	0,9S	90%
Март	0,9Sr	0,9Sr — 0,8S	0,8S	80%
Апрель	0,8Sr	0,8Sr — 0,7S	0,7S	70%
Май	0,7Sr	0,7Sr — 0,6S	0,6S	60%
Июнь	0,6Sr	0,6S r — 0,5S	0,5S	50%
Июль	0,5Sr	0,5Sr	0	0%

Общая сумма выплат составит:

Общая сумма выплат от суммы кредита:

Следовательно, переплата равна 22,5%.

II способ — используем частный случай.

Пусть сумма кредита равна 100 руб.

Долг с начисленными процентами, руб.	Выплата, руб.	Остаток долга, руб.	Остаток долга, %
Февраль	100 * 1,05 = 105	105 — 90 = 15	90	90%
Март	90 * 1,05 = 94,5	94,5 — 80 = 14,5	80	80%
Апрель	80 * 1,05 = 84	84 — 70 = 14	70	70%
Май	70 * 1,05 = 73,5	73,5 — 60 = 13,5	60	60%
Июнь	60 * 1,05 = 66,3	66,3 — 50 = 13	50	50%
Июль	50 * 1,05 = 52,5	52,5	0	0%

Общая сумма выплат:

Следовательно, переплата равна 22,5%.

Задача 2. Рассчитываем наибольшее значение процентов, при котором общая сумма выплат будет меньше заданного числа

15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн руб. Условия его возврата таковы:

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн руб.

Выплата, млн руб.

Остаток долга, млн руб.

Обратите внимание! Ежемесячная выплата рассчитывается как разность между долгом на начало месяца и остатком долга. Следовательно, третий столбец заполняется в последнюю очередь.

Общая суммы выплат:

Обратите внимание! Вычисление следует производить до тысячных.

По условию задачи, r — целое число, следовательно, r = 7%.

Еженедельная рассылка с лучшими материалами «Открытого журнала»

Без минимальной суммы, платы за обслуживание и скрытых комиссий

Для оформления продукта необходим брокерский счёт

проект «Открытие Инвестиции»

Открыть брокерский счёт

Тренировка на учебном счёте

Об «Открытие Инвестиции»

Москва, ул. Летниковская,
д. 2, стр. 4

8 800 500 99 66

Согласие на обработку персональных данных

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Инвестор получил кредит в банке в сумме 150,0 млн. руб. сроком на 3 года под 20% годовых (сложные проценты). Определить сумму погашения долга в конце срока.

S = 150(1+0,2) 3 - 259,2 млн. руб.

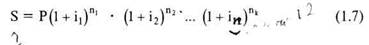
Зачастую банки, предоставляя долгосрочные кредиты, используют изменяющиеся во времени, но заранее фиксированные для каждого периода ставки сложных процентов. В этом случае наращенная сумма может быть определена по формуле:

ip i₂ . Vu) — последовательные значения ставок процентов;

Пр п₂ . n_k — периоды, в течение которых используются соответствующие ставки.

Пример 1.4.

Строительная фирма получила кредит в банке на сумму 100,0 млн. руб. сроком на 5 лет;

процентная ставка по кредиту определена в 10,5% для 1-го года, для 2-го предусмотрена надбавка к процентной ставке в размере 1,5%, для 3-го года и последующих лет — в размере 0,75%.

Определить сумму долга, подлежащую погашению в конце сро
ка займа:

S = 100 • 1,105 • 1,12 • 1,1275 3 = 177,39 млн. руб.

Использование в финансовых вычислениях простых и сложных процентов дает неодинаковые результаты, различия между ними обусловлены сроками сделок.

Так, при равной величине простых и сложных процентных ста-

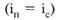
вок при сроке ссуды менее одного года (п < 1) наращен-

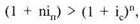ная сумма, вычисленная по простым процентам, будет больше наращенной суммы, вычисленной по сложным процентам, ибо

i_n и i_c — ставки простых и сложных процентов.

При сроке сделки больше года (п > 1) наращение по сложным процентам опережает наращение по простым процентам (1 + ni^) < (1 + i_c) n .

В случае, когда срок финансовой сделки выражен дробным числом, начисление процентов может выполнятся двумя методами:

а) по формуле сложных процентов *

б) смешанным методом

— период сделки; - целое число лет; b — дробная часть года. Пример 1.5.

Инвестор получил кредит в банке в размере 250 млн. руб. со сроком погашения через 2 года и 9 месяцев (2 года и 270 дней), под 9,5% годовых.

Определим полученную им сумму при использовании банком сложных процентов и смешанного метода. При расчете банк счи-

- на сумму возвращенного кредита и уплаченных процентов - 150 450 руб.

(147 500 руб. + 2950 руб.).

Контрольные задания

1. Ситуация. В начале января 2007 г. организацией получен в банке кредит на сумму 2 млн. руб. сроком на три года под 24 % годовых. Кредит предназначен для финансирования строительства торгового центра. Торговый центр введен в эксплуатацию 1 декабря 2007 г. Проценты по кредиту начисляются и выплачиваются в конце каждого месяца.

Задание. Рассчитать сумму ежемесячно выплачиваемых процентов, определить сумму процентов, включаемых в фактические затраты на строительство торгового центра, составить проводки, отражающие получение и возврат кредита, начисление и уплату процентов.

2. Ситуация.Организация получила заем от юридического лица в сумме

500 000 руб. на три месяца. В обеспечение займа организация выдала собственный вексель на сумму 550 000 руб. По истечении трех месяцев организация уплатила по векселю.

Задание. Составить бухгалтерские проводки.

ГОСУДАРСТВЕННАЯ ПОМОЩЬ

Учет бюджетных средств

Бюджетные средства, принятые к бухгалтерскому учету, отражаются в бухгалтерском учете как возникновение целевого финансирования и задолженности по этим средствам. По мере фактического получения средств соответствующие суммы уменьшают задолженность и увеличивают счета учета денежных средств, капитальных вложений и т. п. (п. 7 ЛБУ 13/2000).

Пример 10.10

Организация получила извещение финансирующего органа о выделенных суммах бюджетных средств в размере 150 000 руб. на покрытие расходов по строительству согласно смете. Денежные средства получены.

Составим бухгалтерские проводки:

Дебет 76 «Расчеты с разными дебиторами и кредиторами» Кредит 86 «Целевое финансирование»

- на сумму выделенных бюджетных средств - 150 000 руб.;

Дебет 51 «Расчетные счета» Кредит 76 «Расчеты с разными дебиторами и кредиторами»

- на сумму полученных бюджетных средств - 150 000 руб.

Если бюджетные средства признаются в бухгалтерском учете по мере фактического получения ресурсов, то с возникновением целевого финансирования увеличиваются счета учета денежных средств, капитальных вложений и т. п. (п. 7 ПБУ 13/2000).

Организацией I марта 2007 г. получен в банке кредит в сумме 1 000 000 руб. По условиям договора основная сумма долга должна быть погашена 1 сентября 2008 г. 2 сентября 2007 г. (когда по условиям договора кредита до возврата основной суммы долга осталось 365 дней) долгосрочная задолженность переведена в краткосрочную. 1 сентября 2008 г. (по истечении срока договора) кредит возвращен.

Составим бухгалтерские проводки:

1 марта 2007 г.:

Дебет 51 «Расчетные счета» Кредит 67 «Расчеты по долгосрочным кредитам и займам»

- на сумму полученного кредита - 1 000 000 руб.;

2 сентября 2007 г.:

Дебет 67 «Расчеты по долгосрочным кредитам и займам» Кредит 66 «Расчеты по краткосрочным кредитам и займам»

- на сумму долга, переведенную в состав краткосрочной задолженности,

1 сентября 2008 г.:

Дебет 66 «Расчеты по краткосрочным кредитам и займам» Кредит 51 «Расчетные счета»

- на сумму денежных средств, перечисленных в счет погашения Кредита,

Учет затрат по обслуживанию кредитов и займов

Затраты, связанные с получением и использованием займов и кредитов, включают:

- проценты, причитающиеся к оплате заимодавцам и кредиторам по полученным от них займам и кредитам;

- проценты, дисконт по причитающимся к оплате векселям и облигациям;

- дополнительные затраты, произведенные в связи сполучением займов и кредитов, выпуском и размещением заемных обязательств;

- курсовые разницы, относящиеся на причитающиеся к оплате проценты по займам и кредитам, полученным и выраженным в иностранной валюте или условных денежных единицах, образующиеся начиная с момента начисления процентов по условиям договора до их фактического погашения (перечисления) (п. 11 ПБУ 15/01).

Затраты по полученным займам и кредитам, включаемые в текущие расходы организации, являются ее прочими расходами и подлежат включению в финансовый результат организации (п. 14 ПБУ 15/01).

Причитающиеся по полученным кредитам и займам проценты к уплате отражаются по кредиту счета 66 «Расчеты по краткосрочным кредитам и займам» (67 «Расчеты по долгосрочным кредитам и займам») в корреспонденции с дебетом счета 91 «Прочие доходы и расходы» (Инструкция по применению Плана счетов. Счет 66 «Расчеты по краткосрочным кредитам и займам» (67 «Расчеты по долгосрочным кредитам и займам»)).

Начисление процентов по полученным займам и кредитам организация производит в соответствии с порядком, установленным в договоре займа и (или) кредитном договоре (п. 16 ПБУ 15/01).

Экономические задачи ввели в единый государственный экзамен по математике (профильный уровень) с 2015 года. При их решении у экзаменующихся часто возникают затруднения, ведь в жизни они пока не сталкивались с кредитами и вкладами, а значит, плохо понимают условия задач и действия, выполняемые внутри них.

Разбор типовых задач (задание 17) из ЕГЭ по математике профильного уровня будет полезен не только выпускникам школ, но и любителям прикладных методов в банковской сфере.

Как решать экономические задачи?

Часть экономических задач можно решить универсальным способом — с помощью составления таблицы, которая позволит упорядочить данные по временным интервалам.

Для всех типов задач при составлении таблицы используется единый алгоритм.

Условия задач взяты с сайта РЕШУ ЕГЭ .

Задачи на равные платежи по кредиту

В задачах этого типа заёмщик всегда вносит равные суммы. При решении подобных задач надо следовать ряду советов.

Задача 1. Рассчитываем общую сумму кредита

В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

Какая сумма была взята в банке, если известно, что кредит был полностью погашен тремя равными платежами (то есть за три года)?

S руб. — сумма кредита,
р = 0,31,
r = 131,
В = 69 690 821 руб. — ежегодная выплата.

Долг с начисленными процентами	Выплата	Остаток долга
1	S * r	B	S * r — B
2	(S * r — B) * r	B	(S * r — B) * r — B
3	((S * r — B) * r — B) * r	B	0

По последней строке составляем уравнение:

Далее последовательно раскроем скобки:

Теперь можно подставить числовые данные:

Многолетняя практика по решению реальных экзаменационных вариантов показывает, что числовые данные для задач подбираются неслучайно. Составители могут специально подбирать значения таким образом, чтобы получающиеся при вычислениях дроби можно было сократить. Поэтому, прежде чем взяться за вычисление знаменателя, надо проверить, будет ли число 69 690 821 делиться на 1,31.

Ответ: Общая сумма кредита 124 809 100 руб.

Задача 2. Рассчитываем процент кредита

31 декабря 2020 г. Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на х%), затем Пётр переводит очередной платёж. Если он будет платить каждый год по 2 592 000 руб., то выплатит долг за четыре года. Если по 4 392 000 руб., то за два года. Под какой процент Пётр взял деньги в банке?

S тыс. руб. — сумма кредита,
Х% — в десятичной дроби,
r = 1 + a,
А = 2 592 000 руб. — ежегодный платёж 1,
В = 4 392 000 руб. — ежегодный платёж 2.

Долг с начисленными процентами	Выплата	Остаток долга
1	S * r	А	S * r — А
2	(S * r — А) * r	А	(S * r — А) * r — А
3	((S * r — А) * r — А) * r	А	((S * r — А) * r — А) * r — А
4	(((S * r — А) * r — А) * r — A) * r	А	0
1	S * r	B	S * r — B
2	(S * r — B) * r	B	0